خوارزمية بيلمان فورد هي خوارزمية أقصر مسار أحادية المصدر. تُستخدم هذه الخوارزمية للعثور على أقصر مسافة من الرأس الفردي إلى جميع القمم الأخرى للرسم البياني الموزون. هناك العديد من الخوارزميات الأخرى المستخدمة للعثور على أقصر مسار مثل خوارزمية Dijkstra، وما إلى ذلك. إذا كان الرسم البياني الموزون يحتوي على قيم الوزن السالبة، فإن خوارزمية Dijkstra لا تؤكد ما إذا كانت تنتج الإجابة الصحيحة أم لا. وعلى النقيض من خوارزمية ديكسترا، تضمن خوارزمية بيلمان فورد الإجابة الصحيحة حتى لو كان الرسم البياني الموزون يحتوي على قيم الوزن السالبة.
حكم هذه الخوارزمية
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
النظر في الرسم البياني أدناه:
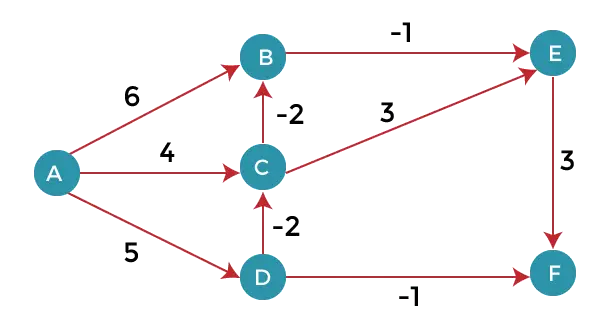
كما نلاحظ في الرسم البياني أعلاه أن بعض الأوزان سلبية. يحتوي الرسم البياني أعلاه على 6 رؤوس، لذا سنستمر في الاسترخاء حتى القمم الخمسة. هنا، سوف نقوم بإرخاء جميع الحواف 5 مرات. سيتم تكرار الحلقة 5 مرات للحصول على الإجابة الصحيحة. إذا تم تكرار الحلقة أكثر من 5 مرات فإن الإجابة ستكون نفسها أيضًا، أي لن يكون هناك تغيير في المسافة بين القمم.
الاسترخاء يعني:
ياسمين ديفيس عندما كانت طفلة
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
د(ت) = 0 + 6 = 6
وبالتالي فإن مسافة الرأس B هي 6.
النظر في الحافة (أ، ج). قم بالإشارة إلى الرأس 'A' بالرمز 'u' والرأس 'C' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 0
د(ت) = ∞
ج(ش، الخامس) = 4
بما أن (0 + 4) أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 0 + 4 = 4
وبالتالي فإن مسافة الرأس C هي 4.
النظر في الحافة (أ، د). يُشار إلى الرأس 'A' بالرمز 'u' والرأس 'D' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 0
د(ت) = ∞
ج(ش، الخامس) = 5
بما أن (0 + 5) أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 0 + 5 = 5
وبالتالي فإن مسافة الرأس D هي 5.
النظر في الحافة (B، E). يُشار إلى الرأس 'B' بالرمز 'u' والرأس 'E' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 6
د(ت) = ∞
ج(ش، الخامس) = -1
بما أن (6 - 1) أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 6 - 1= 5
وبالتالي فإن مسافة الرأس E هي 5.
النظر في الحافة (C، E). قم بالإشارة إلى الرأس 'C' بالرمز 'u' والرأس 'E' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 4
د(ت) = 5
ج(ش، الخامس) = 3
وبما أن (4 + 3) أكبر من 5، فلن يكون هناك تحديث. القيمة عند الرأس E هي 5.
خذ بعين الاعتبار الحافة (D، C). قم بالإشارة إلى الرأس 'D' بالرمز 'u' والرأس 'C' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 5
د(ت) = 4
ج(ش، الخامس) = -2
بما أن (5 -2) أقل من 4، فقم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 5 - 2 = 3
وبالتالي فإن مسافة الرأس C هي 3.
خذ بعين الاعتبار الحافة (D، F). قم بالإشارة إلى الرأس 'D' بالرمز 'u' والرأس 'F' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 5
د(ت) = ∞
ج(ش، الخامس) = -1
أرقام الأبجدية
بما أن (5 -1) أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 5 - 1 = 4
وبالتالي فإن مسافة الرأس F هي 4.
النظر في الحافة (E، F). يُشار إلى الرأس 'E' بالرمز 'u' والرأس 'F' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 5
د(ت) = ∞
ج(ش، الخامس) = 3
وبما أن (5 + 3) أكبر من 4، فلن يكون هناك تحديث على قيمة مسافة الرأس F.
خذ بعين الاعتبار الحافة (C، B). يُشار إلى الرأس 'C' بالرمز 'u' والرأس 'B' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 3
د(ت) = 6
ج(ش، الخامس) = -2
بما أن (3 - 2) أقل من 6، فقم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 3 - 2 = 1
وبالتالي فإن مسافة الرأس B هي 1.
الآن اكتمل التكرار الأول. ننتقل إلى التكرار الثاني.
التكرار الثاني:
في التكرار الثاني، نتحقق مرة أخرى من جميع الحواف. الحافة الأولى هي (أ، ب). وبما أن (0 + 6) أكبر من 1، فلن يكون هناك تحديث في الرأس B.
الحافة التالية هي (أ، ج). وبما أن (0 + 4) أكبر من 3، فلن يكون هناك تحديث في الرأس C.
الحافة التالية هي (أ، د). وبما أن (0 + 5) يساوي 5، فلن يكون هناك تحديث في الرأس D.
الحافة التالية هي (B، E). بما أن (1 - 1) يساوي 0 وهو أقل من 5، لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(ه) = د(ب) +ج(ب، ه)
= 1 - 1 = 0
الحافة التالية هي (C، E). وبما أن (3 + 3) يساوي 6 وهو أكبر من 5، فلن يكون هناك تحديث في الرأس E.
الحافة التالية هي (D، C). وبما أن (5 - 2) يساوي 3، فلن يكون هناك تحديث في الرأس C.
الحافة التالية هي (D، F). بما أن (5 - 1) يساوي 4 لذلك لن يكون هناك تحديث في الرأس F.
الحافة التالية هي (E، F). وبما أن (5 + 3) يساوي 8 وهو أكبر من 4، فلن يكون هناك تحديث في الرأس F.
الحافة التالية هي (C، B). بما أن (3 - 2) يساوي 1` لذلك لن يكون هناك تحديث في الرأس B.

التكرار الثالث
سنقوم بنفس الخطوات التي قمنا بها في التكرارات السابقة. وسوف نلاحظ أنه لن يكون هناك أي تحديث في مسافة القمم.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
تعقيد الوقت
سيكون التعقيد الزمني لخوارزمية بيلمان فورد هو O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
د(ت) = 0 + 5 = 5
وبالتالي فإن مسافة الرأس 3 هي 5.
النظر في الحافة (1، 2). يُشار إلى الرأس '1' بالرمز 'u' والرأس '2' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 0
د(ت) = ∞
ج(ش، الخامس) = 4
بما أن (0 + 4) أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 0 + 4 = 4
وبالتالي فإن مسافة الرأس 2 هي 4.
النظر في الحافة (3، 2). قم بالإشارة إلى الرأس '3' بالرمز 'u' والرأس '2' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 5
د(ت) = 4
ج(ش، الخامس) = 7
وبما أن (5 + 7) أكبر من 4، فلن يكون هناك تحديث في الرأس 2.
النظر في الحافة (2، 4). قم بالإشارة إلى الرأس '2' بالرمز 'u' والرأس '4' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 4
د(ت) = ∞
ج(ش، الخامس) = 7
بما أن (4 + 7) يساوي 11 وهو أقل من ∞، لذا قم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 4 + 7 = 11
وبالتالي فإن مسافة الرأس 4 هي 11.
النظر في الحافة (4، 3). قم بالإشارة إلى الرأس '4' بالرمز 'u' والرأس '3' بالرمز 'v'. الآن استخدم صيغة الاسترخاء:
د(ش) = 11
د(ت) = 5
ج(ش، الخامس) = -15
بما أن (11 - 15) يساوي -4 وهو أقل من 5، فقم بالتحديث
d(v) = d(u) + c(u , v)
د(ت) = 11 - 15 = -4
وبالتالي فإن مسافة الرأس 3 هي -4.
الآن ننتقل إلى التكرار الثاني.
التكرار الثاني
الآن، مرة أخرى سوف نتحقق من جميع الحواف. الحافة الأولى هي (1، 3). وبما أن (0 + 5) يساوي 5 وهو أكبر من -4 فلن يكون هناك تحديث في الرأس 3.
الحافة التالية هي (1، 2). وبما أن (0 + 4) يساوي 4، فلن يكون هناك تحديث في الرأس 2.
معرف الاستعلام
الحافة التالية هي (3، 2). بما أن (-4 + 7) يساوي 3 وهو أقل من 4، لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(2) = د(3) +ج(3، 2)
= -4 + 7 = 3
وبالتالي فإن القيمة عند الرأس 2 هي 3.
الحافة التالية هي (2، 4). بما أن (3+7) يساوي 10 وهو أقل من 11، لذا قم بالتحديث
د(ت) = د(ش) + ج(ش، ت)
د(4) = د(2) +ج(2، 4)
= 3 + 7 = 10
وبالتالي فإن القيمة عند الرأس 4 هي 10.
الصورة كخلفية في CSS
الحافة التالية هي (4، 3). بما أن (10 - 15) يساوي -5 وهو أقل من -4 لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(3) = د(4) +ج(4، 3)
= 10 - 15 = -5
ولذلك، فإن القيمة عند الرأس 3 هي -5.
الآن ننتقل إلى التكرار الثالث.
التكرار الثالث
الآن مرة أخرى سوف نتحقق من جميع الحواف. الحافة الأولى هي (1، 3). وبما أن (0 + 5) يساوي 5 وهو أكبر من -5 فلن يكون هناك تحديث في الرأس 3.
الحافة التالية هي (1، 2). وبما أن (0 + 4) يساوي 4 وهو أكبر من 3، فلن يكون هناك تحديث في الرأس 2.
الحافة التالية هي (3، 2). بما أن (-5 + 7) يساوي 2 وهو أقل من 3، لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(2) = د(3) +ج(3، 2)
= -5 + 7 = 2
وبالتالي فإن القيمة عند الرأس 2 هي 2.
الحافة التالية هي (2، 4). بما أن (2 + 7) يساوي 9 وهو أقل من 10، لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(4) = د(2) +ج(2، 4)
= 2 + 7 = 9
وبالتالي فإن القيمة عند الرأس 4 هي 9.
الحافة التالية هي (4، 3). بما أن (9 - 15) يساوي -6 وهو أقل من -5 لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(3) = د(4) +ج(4، 3)
= 9 - 15 = -6
وبالتالي فإن القيمة عند الرأس 3 هي -6.

نظرًا لأن الرسم البياني يحتوي على 4 رؤوس، وفقًا لخوارزمية بيلمان فورد، سيكون هناك 3 تكرارات فقط. إذا حاولنا أداء 4ذبالتكرار على الرسم البياني، يجب ألا تتغير مسافة القمم من الرأس المحدد. إذا اختلفت المسافة، فهذا يعني أن خوارزمية بيلمان فورد لا تقدم الإجابة الصحيحة.
4ذتكرار
الحافة الأولى هي (1، 3). وبما أن (0 +5) يساوي 5 وهو أكبر من -6 فلن يكون هناك أي تغيير في الرأس 3.
الحافة التالية هي (1، 2). وبما أن (0 + 4) أكبر من 2 فلن يكون هناك تحديث.
الحافة التالية هي (3، 2). بما أن (-6 + 7) يساوي 1 وهو أقل من 3، لذا قم بالتحديث:
د(ت) = د(ش) + ج(ش، ت)
د(2) = د(3) +ج(3، 2)
= -6 + 7 = 1
في هذه الحالة، يتم تحديث قيمة الرأس. لذلك، نستنتج أن خوارزمية بيلمان فورد لا تعمل عندما يحتوي الرسم البياني على دورة الوزن السلبي.
وبالتالي فإن القيمة عند الرأس 2 هي 1.
