سنناقش في هذا القسم طريقة تحويل NFA إلى DFA المكافئ له. في NFA، عندما يتم إعطاء مدخلات محددة للحالة الحالية، ينتقل الجهاز إلى حالات متعددة. يمكن أن تحتوي على صفر أو حركة واحدة أو أكثر من حركة واحدة على رمز إدخال معين. من ناحية أخرى، في DFA، عندما يتم إعطاء مدخلات محددة للحالة الحالية، ينتقل الجهاز إلى حالة واحدة فقط. لدى DFA حركة واحدة فقط على رمز الإدخال المحدد.
Let، M = (Q، ∑، δ، q0، F) هو NFA الذي يقبل اللغة L (M). يجب أن يكون هناك DFA مكافئ يُشار إليه بـ M' = (Q'، ∑'، q0'، δ'، F') بحيث L(M) = L(M').
خطوات تحويل NFA إلى DFA:
الخطوة 1: في البداية Q' = ϕ
الخطوة 2: أضف q0 من NFA إلى Q'. ثم ابحث عن التحولات من حالة البداية هذه.
الخطوه 3: في Q'، ابحث عن مجموعة الحالات المحتملة لكل رمز إدخال. إذا لم تكن مجموعة الحالات هذه في Q'، فقم بإضافتها إلى Q'.
10 من 60
الخطوة 4: في DFA، ستكون الحالة النهائية هي جميع الحالات التي تحتوي على F (الحالات النهائية لـ NFA)
الأبجدية والأرقام
مثال 1:
قم بتحويل NFA المحدد إلى DFA.
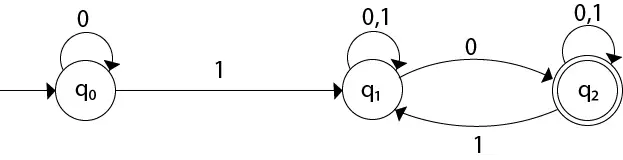
حل: بالنسبة لمخطط الانتقال المحدد، سنقوم أولاً بإنشاء جدول الانتقال.
| ولاية | 0 | 1 |
|---|---|---|
| →س0 | س0 | س1 |
| س1 | {q1, q2} | س1 |
| *q2 | q2 | {q1, q2} |
الآن سوف نحصل على انتقال δ للحالة q0.
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
يتم الحصول على الانتقال δ للحالة q1 على النحو التالي:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
يتم الحصول على الانتقال δ للحالة q2 على النحو التالي:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
الآن سوف نحصل على انتقال δ على [q1، q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] الحالة [q1, q2] هي الحالة النهائية أيضًا لأنها تحتوي على الحالة النهائية q2. سيكون الجدول الانتقالي لـ DFA الذي تم إنشاؤه هو:
مهم
| ولاية | 0 | 1 |
|---|---|---|
| →[س0] | [س0] | [س1] |
| [س1] | [q1, q2] | [س1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
مخطط الانتقال سيكون:

يمكن حذف الحالة q2 لأن q2 هي حالة لا يمكن الوصول إليها.
مثال 2:
قم بتحويل NFA المحدد إلى DFA.

حل: بالنسبة لمخطط الانتقال المحدد، سنقوم أولاً بإنشاء جدول الانتقال.
خريطة متكررة جافا
| ولاية | 0 | 1 |
|---|---|---|
| →س0 | {س0، س1} | {س1} |
| *س1 | ϕ | {س0، س1} |
الآن سوف نحصل على انتقال δ للحالة q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] يتم الحصول على الانتقال δ للحالة q1 على النحو التالي:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
الآن سوف نحصل على انتقال δ على [q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] بصورة مماثلة،
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] كما هو الحال في NFA المحدد، q1 هي حالة نهائية، ثم في DFA أينما وجدت q1 تصبح تلك الحالة حالة نهائية. وبالتالي في DFA، الحالات النهائية هي [q1] و [q0، q1]. لذلك مجموعة الحالات النهائية F = {[q1]، [q0، q1]}.
سيكون الجدول الانتقالي لـ DFA الذي تم إنشاؤه هو:
| ولاية | 0 | 1 |
|---|---|---|
| →[س0] | [س0، س1] | [س1] |
| *[س1] | ϕ | [س0، س1] |
| *[س0، س1] | [س0، س1] | [س0، س1] |
مخطط الانتقال سيكون:
طريقة جافا الرئيسية

حتى يمكننا تغيير اسم ولايات DFA.
يفترض
A = [q0] B = [q1] C = [q0, q1]
بهذه الأسماء الجديدة سيكون DFA على النحو التالي:

