- يشير DFA إلى أتمتة حتمية محدودة. الحتمية تشير إلى تفرد الحساب. تُسمى الآلات الآلية المحدودة بالآلات الحتمية المحدودة إذا كان الجهاز يقرأ سلسلة إدخال رمزًا واحدًا في كل مرة.
- في DFA، يوجد مسار واحد فقط لإدخال محدد من الحالة الحالية إلى الحالة التالية.
- لا يقبل DFA النقل الفارغ، أي أنه لا يمكن لـ DFA تغيير الحالة دون أي حرف إدخال.
- يمكن أن يحتوي DFA على حالات نهائية متعددة. يتم استخدامه في التحليل المعجمي في المترجم.
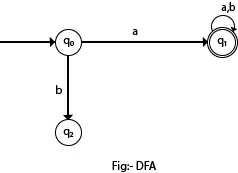
في الرسم البياني التالي، يمكننا أن نرى أنه من الحالة q0 للمدخل a، هناك مسار واحد فقط يتجه إلى q1. وبالمثل، من q0، هناك مسار واحد فقط للإدخال b يتجه إلى q2.
التعريف الرسمي لـ DFA
DFA عبارة عن مجموعة من 5 صفوف كما وصفناها في تعريف FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
يمكن تعريف وظيفة الانتقال على النحو التالي:
δ: Q x ∑→Q
التمثيل الرسومي لـ DFA
يمكن تمثيل DFA بواسطة رسوم بيانية تسمى مخطط الحالة. بحيث:
- يتم تمثيل الدولة بالقمم.
- يُظهر القوس المسمى بحرف الإدخال التحولات.
- يتم تمييز الحالة الأولية بسهم.
- يتم الإشارة إلى الحالة النهائية بدائرة مزدوجة.
مثال 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} حل:
مخطط الانتقال:

الجدول الانتقالي:
| الحالة الحالية | الحالة التالية للإدخال 0 | حالة الإدخال التالية 1 |
|---|---|---|
| →س0 | س0 | س1 |
| س1 | q2 | س1 |
| *q2 | q2 | q2 |
مثال 2:
DFA مع ∑ = {0, 1} يقبل كل شيء بدءًا من 0.
حل:

توضيح:
- في الرسم البياني أعلاه، يمكننا أن نرى أنه عند إعطاء 0 كمدخل إلى DFA في الحالة q0، يغير DFA الحالة إلى q1 وينتقل دائمًا إلى الحالة النهائية q1 عند بدء الإدخال 0. يمكنه قبول 00، 01، 000، 001... .إلخ. لا يمكنه قبول أي سلسلة تبدأ بالرقم 1، لأنها لن تصل أبدًا إلى الحالة النهائية لسلسلة تبدأ بالرقم 1.
مثال 3:
DFA مع ∑ = {0, 1} يقبل كل ما ينتهي بـ 0.
حل:

توضيح:
في الرسم البياني أعلاه، يمكننا أن نرى أنه عند إعطاء 0 كمدخل إلى DFA في الحالة q0، يغير DFA الحالة إلى q1. يمكنه قبول أي سلسلة تنتهي بالرقم 0 مثل 00، 10، 110، 100....إلخ. لا يمكن قبول أي سلسلة تنتهي بـ 1، لأنها لن تنتقل أبدًا إلى الحالة النهائية q1 عند إدخال واحد، لذلك لن يتم قبول السلسلة التي تنتهي بـ 1 أو سيتم رفضها.
