شجرة التعبير هي شجرة تستخدم لتمثيل التعبيرات المختلفة. يتم استخدام بنية بيانات الشجرة لتمثيل البيانات التعبيرية. في هذه الشجرة، تشير العقدة الداخلية دائمًا إلى عوامل التشغيل.
- تشير العقد الورقية دائمًا إلى المعاملات.
- يتم تنفيذ العمليات دائمًا على هذه المعاملات.
- العامل الموجود في عمق الشجرة يحظى دائمًا بالأولوية القصوى.
- المشغل، الذي ليس كثيرًا في عمق الشجرة، يكون دائمًا في أدنى أولوية مقارنة بالمشغلين الموجودين في العمق.
- سيظهر المعامل دائمًا على عمق الشجرة؛ ومن هنا يعتبر الأولوية القصوى بين جميع المشغلين.
- باختصار، يمكننا تلخيص ذلك بأن القيمة الموجودة على عمق الشجرة هي ذات الأولوية القصوى مقارنة بالعوامل الأخرى الموجودة في أعلى الشجرة.
- الاستخدام الرئيسي لأشجار التعبير هذه هو استخدامها تقييم وتحليل و يُعدِّل التعبيرات المختلفة.
- يتم استخدامه أيضًا لمعرفة ارتباط كل عامل في التعبير.
- على سبيل المثال، عامل التشغيل + هو الاقتران الأيسر و/ هو الاقتران الأيمن.
- تم حل معضلة هذا الارتباط باستخدام أشجار التعبير.
- يتم تشكيل أشجار التعبير هذه باستخدام قواعد نحوية خالية من السياق.
- لقد قمنا بربط قاعدة في القواعد النحوية الخالية من السياق أمام كل إنتاج نحوي.
- تُعرف هذه القواعد أيضًا باسم القواعد الدلالية، وباستخدام هذه القواعد الدلالية، يمكننا بسهولة إنشاء أشجار التعبير.
- إنه أحد الأجزاء الرئيسية لتصميم المترجم وينتمي إلى مرحلة التحليل الدلالي.
- في هذا التحليل الدلالي، سنستخدم الترجمات الموجهة نحو بناء الجملة، وفي شكل مخرجات، سننتج شجرة التحليل المشروحة.
- شجرة التحليل المشروحة ليست سوى تحليل بسيط مرتبط بسمة النوع وكل قاعدة إنتاج.
- الهدف الرئيسي من استخدام أشجار التعبير هو إنشاء تعبيرات معقدة ويمكن تقييمها بسهولة باستخدام أشجار التعبير هذه.
- إنه غير قابل للتغيير، وبمجرد إنشاء شجرة تعبير، لا يمكننا تغييرها أو تعديلها بشكل أكبر.
- لإجراء المزيد من التعديلات، يلزم إنشاء شجرة التعبير الجديدة بالكامل.
- يتم استخدامه أيضًا لحل تقييم تعبيرات postfix وprefix وinfix.
تلعب أشجار التعبير دورًا مهمًا جدًا في تمثيل مستوى اللغة رمز في شكل بيانات، والتي يتم تخزينها بشكل أساسي في بنية تشبه الشجرة. يتم استخدامه أيضًا في تمثيل الذاكرة لـ لامدا تعبير. باستخدام بنية بيانات الشجرة، يمكننا التعبير عن تعبير لامدا بشكل أكثر شفافية وصراحة. يتم إنشاؤه أولاً لتحويل مقطع التعليمات البرمجية إلى مقطع البيانات بحيث يمكن تقييم التعبير بسهولة.
شجرة التعبير عبارة عن شجرة ثنائية حيث تتوافق كل عقدة خارجية أو عقدة ورقية مع المعامل وكل عقدة داخلية أو أصل تتوافق مع العوامل، لذلك على سبيل المثال شجرة التعبير لـ 7 + ((1+8)*3) ستكون:
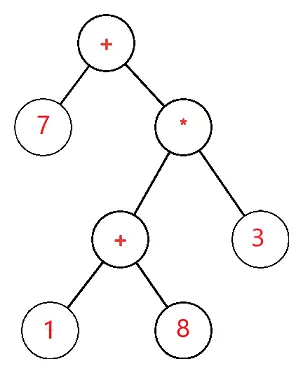
دع S تكون شجرة التعبير
إذا لم تكن S فارغة، إذن
إذا كانت S.value مُعاملًا، إذن
إرجاع قيمة S
س = حل (S.left)
ص = حل (S. يمين)
إرجاع الحساب (x، y، S.value)
هنا في المثال أعلاه، استخدمت شجرة التعبير قواعد نحوية خالية من السياق.
لدينا بعض الإنتاجات المرتبطة ببعض قواعد الإنتاج في هذا النحو، والمعروفة بشكل رئيسي باسم القواعد الدلالية . يمكننا تحديد النتيجة المنتجة من قواعد الإنتاج المقابلة باستخدام هذه القواعد الدلالية. لقد استخدمنا هنا معلمة القيمة، والتي ستقوم بحساب النتيجة وإعادتها إلى رمز بداية القواعد. سيحسب S.left الابن الأيسر للعقدة، وبالمثل، يمكن حساب الطفل الأيمن للعقدة باستخدام المعلمة S.right.
استخدام شجرة التعبير
- الهدف الرئيسي من استخدام أشجار التعبير هو إنشاء تعبيرات معقدة ويمكن تقييمها بسهولة باستخدام أشجار التعبير هذه.
- يتم استخدامه أيضًا لمعرفة ارتباط كل عامل في التعبير.
- يتم استخدامه أيضًا لحل تقييم تعبيرات postfix وprefix وinfix.
تنفيذ شجرة التعبير
لتنفيذ شجرة التعبير وكتابة برنامجها، سيُطلب منا استخدام بنية بيانات المكدس.
كما نعلم أن المكدس يعتمد على مبدأ ما يدخل أولاً يخرج أولاً LIFO، فإن عنصر البيانات الذي تم دفعه مؤخرًا إلى المكدس قد تم إخراجه كلما لزم الأمر. لتنفيذه، يتم استخدام العمليتين الرئيسيتين للمكدس، والدفع والبوب. باستخدام عملية الدفع، سنقوم بدفع عنصر البيانات إلى المكدس، وباستخدام عملية البوب، سنقوم بإزالة عنصر البيانات من المكدس.
الوظائف الرئيسية للمكدس في تنفيذ شجرة التعبير:
أولاً، سنقوم بمسح التعبير المحدد من اليسار إلى اليمين، ثم نتحقق من الحرف المحدد واحدًا تلو الآخر،
- إذا كان الحرف الممسوح ضوئيًا مُعاملًا، فسنطبق عملية الدفع وندفعه إلى المكدس.
- إذا كان الحرف الذي تم مسحه ضوئيًا عامل تشغيل، فسنطبق عليه عملية البوب لإزالة القيمتين من المكدس لجعلهما تابعين له، وبعد ذلك سندفع العقدة الأصلية الحالية إلى المكدس.
تنفيذ شجرة التعبير في لغة البرمجة C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> مخرجات البرنامج أعلاه هي:
X + Y * Z / W
تنفيذ شجرة التعبير في لغة البرمجة C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> مخرجات البرنامج أعلاه هي:
X + Y * Z / W
تنفيذ شجرة التعبير في لغة برمجة جافا
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 