الطريقة الجشعة هي إحدى الاستراتيجيات مثل فرق تسد المستخدمة لحل المشكلات. يتم استخدام هذه الطريقة لحل مشاكل التحسين. مشكلة التحسين هي مشكلة تتطلب الحد الأقصى أو الحد الأدنى من النتائج. دعونا نفهم من خلال بعض المصطلحات.
الطريقة الجشعة هي الطريقة الأبسط والمباشرة. إنها ليست خوارزمية، ولكنها تقنية. وتتمثل المهمة الرئيسية لهذا النهج في اتخاذ القرار على أساس المعلومات المتاحة حاليا. ومهما كانت المعلومات الحالية موجودة، يتم اتخاذ القرار دون القلق بشأن تأثير القرار الحالي في المستقبل.
ما هو const في جافا
تُستخدم هذه التقنية بشكل أساسي لتحديد الحل الممكن الذي قد يكون أو لا يكون الأمثل. الحل الممكن هو مجموعة فرعية تفي بالمعايير المحددة. الحل الأمثل هو الحل الأفضل والأكثر ملاءمة في المجموعة الفرعية. في حالة الجدوى، إذا كان هناك أكثر من حل يحقق المعايير المحددة، فسيتم اعتبار تلك الحلول مجدية، في حين أن الحل الأمثل هو الحل الأفضل بين جميع الحلول.
خصائص الطريقة الجشعة
وفيما يلي خصائص الطريقة الجشعة:
- لبناء الحل بالطريقة المثلى، تقوم هذه الخوارزمية بإنشاء مجموعتين حيث تحتوي مجموعة واحدة على جميع العناصر المختارة، ومجموعة أخرى تحتوي على العناصر المرفوضة.
- تقوم الخوارزمية الجشعة باتخاذ خيارات محلية جيدة على أمل أن يكون الحل ممكنًا أو مثاليًا.
مكونات الخوارزمية الجشعة
المكونات التي يمكن استخدامها في الخوارزمية الجشعة هي:
إذا كان بيان آخر في Java
تطبيقات خوارزمية الجشع
- يتم استخدامه للعثور على أقصر طريق.
- يتم استخدامه للعثور على الحد الأدنى من الشجرة الممتدة باستخدام خوارزمية prim أو خوارزمية Kruskal.
- يتم استخدامه في التسلسل الوظيفي مع الموعد النهائي.
- تُستخدم هذه الخوارزمية أيضًا لحل مشكلة الحقيبة الكسرية.
الكود الزائف لخوارزمية الجشع
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } ما ورد أعلاه هو الخوارزمية الجشعة. في البداية، يتم تعيين الحل بقيمة صفر. نقوم بتمرير المصفوفة وعدد العناصر في الخوارزمية الجشعة. داخل حلقة for، نختار العنصر واحدًا تلو الآخر ونتحقق مما إذا كان الحل ممكنًا أم لا. إذا كان الحل ممكنا، فإننا نقوم بإجراء الاتحاد.
دعونا نفهم من خلال مثال.
لنفترض أن هناك مشكلة 'P'. أريد السفر من A إلى B كما هو موضح أدناه:
ف : أ → ب
المشكلة هي أنه يتعين علينا السفر في هذه الرحلة من A إلى B. هناك حلول مختلفة للانتقال من A إلى B. يمكننا الانتقال من A إلى B عن طريق المشي، السيارة، الدراجة، القطار، الطائرة وما إلى ذلك. هناك قيد في الرحلة وهو أنه يتعين علينا قطع هذه الرحلة خلال 12 ساعة. إذا ذهبت بالقطار أو الطائرة، عندها فقط يمكنني قطع هذه المسافة خلال 12 ساعة. هناك العديد من الحلول لهذه المشكلة ولكن هناك حلان فقط يلبيان القيد.
كيفية تحويل str إلى int
إذا قلنا أنه يتعين علينا تغطية الرحلة بأقل تكلفة. وهذا يعني أنه يتعين علينا قطع هذه المسافة بأقل قدر ممكن، لذلك تُعرف هذه المشكلة بمشكلة التقليل. حتى الآن، لدينا حلان ممكنان، أحدهما بالقطار والآخر بالطائرة. وبما أن السفر بالقطار سيؤدي إلى أقل تكلفة لذلك فهو الحل الأمثل. الحل الأمثل هو أيضًا الحل الممكن، ولكن تقديم أفضل نتيجة بحيث يكون هذا الحل هو الحل الأمثل بأقل تكلفة. لن يكون هناك سوى حل أمثل واحد.
المشكلة التي تتطلب الحد الأدنى أو الحد الأقصى للنتيجة تُعرف هذه المشكلة بمشكلة التحسين. تعد طريقة الجشع إحدى الاستراتيجيات المستخدمة لحل مشكلات التحسين.
عيوب استخدام خوارزمية الجشع
تتخذ الخوارزمية الجشعة قرارات بناءً على المعلومات المتاحة في كل مرحلة دون النظر إلى المشكلة الأوسع. لذلك، قد يكون هناك احتمال أن الحل الجشع لا يعطي الحل الأفضل لكل مشكلة.
ويتبع الاختيار الأمثل المحلي في كل مرحلة بهدف إيجاد الأمثل العالمي. دعونا نفهم من خلال مثال.
خذ بعين الاعتبار الرسم البياني الموضح أدناه:
قم بتشغيل جافا
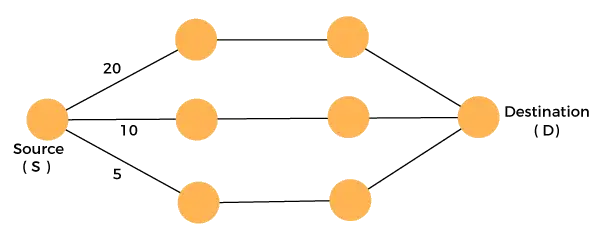
علينا أن نسافر من المصدر إلى الوجهة بأقل تكلفة. نظرًا لأن لدينا ثلاثة حلول مجدية لها مسارات تكلفة مثل 10 و20 و5. 5 هو الحد الأدنى لمسار التكلفة لذا فهو الحل الأمثل. وهذا هو الأمثل المحلي، وبهذه الطريقة نجد الأمثل المحلي في كل مرحلة لنتمكن من حساب الحل الأمثل الشامل.
