ما هو الكومة؟

الكومة عبارة عن شجرة ثنائية كاملة، والشجرة الثنائية هي شجرة يمكن أن تحتوي فيها العقدة على طفلين كحد أقصى. قبل معرفة المزيد عن الكومة، ما هي الشجرة الثنائية الكاملة؟

الشجرة الثنائية الكاملة هي شجرة ثنائية حيث يجب ملء جميع المستويات باستثناء المستوى الأخير، أي العقدة الورقية بالكامل، ويجب ضبط جميع العقد على اليسار.

دعونا نفهم من خلال مثال.

ميغابايت مقابل غيغابايت

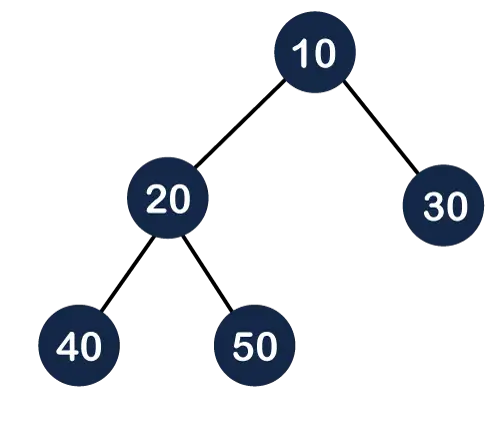
في الشكل أعلاه، نلاحظ أن جميع العقد الداخلية مملوءة بالكامل باستثناء العقدة الورقية؛ لذلك يمكننا القول أن الشجرة المذكورة أعلاه هي شجرة ثنائية كاملة.

يوضح الشكل أعلاه أن جميع العقد الداخلية مملوءة بالكامل باستثناء العقدة الورقية، ولكن تتم إضافة العقد الورقية في الجزء الأيمن؛ ولذلك، فإن الشجرة المذكورة أعلاه ليست شجرة ثنائية كاملة.

ملاحظة: شجرة الكومة عبارة عن بنية بيانات شجرة ثنائية متوازنة خاصة حيث تتم مقارنة العقدة الجذرية مع أبنائها وترتيبها وفقًا لذلك.

كيف يمكننا ترتيب العقد في الشجرة؟

هناك نوعان من الكومة:

• مين كومة
• ماكس الكومة

الحد الأدنى من الكومة: يجب أن تكون قيمة العقدة الأصلية أقل من أو تساوي أيًا من أبنائها.

أو

بمعنى آخر، يمكن تعريف الكومة الصغيرة على أنها، لكل عقدة i، تكون قيمة العقدة i أكبر من أو تساوي قيمتها الأصلية باستثناء العقدة الجذرية. رياضياً يمكن تعريفه على النحو التالي:

أ[الأصل (ط)]<= a[i]< strong>

دعونا نفهم الكومة الصغيرة من خلال مثال.

في الشكل أعلاه، 11 هي العقدة الجذرية، وقيمة العقدة الجذرية أقل من قيمة جميع العقد الأخرى (الطفل الأيسر أو الابن الأيمن).

ماكس كومة: قيمة العقدة الأصلية أكبر من أو تساوي أبنائها.

أو

بمعنى آخر، يمكن تعريف الكومة القصوى لكل عقدة i؛ قيمة العقدة i أقل من أو تساوي قيمتها الأصلية باستثناء العقدة الجذرية. رياضياً يمكن تعريفه على النحو التالي:

أ[الوالد(i)] >= أ[i]

الشجرة المذكورة أعلاه هي شجرة الكومة القصوى لأنها تلبي خاصية الكومة القصوى. الآن، دعونا نرى تمثيل المصفوفة للكومة القصوى.

تعقيد الوقت في ماكس الكومة

إجمالي عدد المقارنات المطلوبة في الكومة القصوى يكون وفقًا لارتفاع الشجرة. يتم دائمًا تسجيل ارتفاع الشجرة الثنائية الكاملة؛ ولذلك، فإن التعقيد الزمني سيكون أيضًا O(logn).

خوارزمية عملية الإدراج في الكومة القصوى.

 // algorithm to insert an element in the max heap. insertHeap(A, n, value) { n=n+1; // n is incremented to insert the new element A[n]=value; // assign new value at the nth position i = n; // assign the value of n to i // loop will be executed until i becomes 1. while(i&gt;1) { parent= floor value of i/2; // Calculating the floor value of i/2 // Condition to check whether the value of parent is less than the given node or not if(A[parent] <a[i]) { swap(a[parent], a[i]); i="parent;" } else return; < pre> <p> <strong>Let&apos;s understand the max heap through an example</strong> .</p> <p>In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.</p> <p> <strong>Insertion in the Heap tree</strong> </p> <p> <strong>44, 33, 77, 11, 55, 88, 66</strong> </p> <p>Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:</p> <ul> <li>First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.</li> <li>Secondly, the value of the parent node should be greater than the either of its child.</li> </ul> <p> <strong>Step 1:</strong> First we add the 44 element in the tree as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-5.webp" alt="Heap Data Structure"> <p> <strong>Step 2:</strong> The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-6.webp" alt="Heap Data Structure"> <p> <strong>Step 3:</strong> The next element is 77 and it will be added to the right of the 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-7.webp" alt="Heap Data Structure"> <p>As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-8.webp" alt="Heap Data Structure"> <p> <strong>Step 4:</strong> The next element is 11. The node 11 is added to the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-9.webp" alt="Heap Data Structure"> <p> <strong>Step 5:</strong> The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-10.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below:< p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-11.webp" alt="Heap Data Structure"> <p> <strong>Step 6:</strong> The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-12.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:< p> <p>Again, it is violating the max heap property because 88&gt;77 so we will swap these two values as shown below:</p> <p> <strong>Step 7:</strong> The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:</p> <p>In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.</p> <p> <strong>Deletion in Heap Tree</strong> </p> <p>In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.</p> <p> <strong>Let&apos;s understand the deletion through an example.</strong> </p> <p> <strong>Step 1</strong> : In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:</p> <p>Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:</p> <p>Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.</p> <p> <strong>Algorithm to heapify the tree</strong> </p> <pre> MaxHeapify(A, n, i) { int largest =i; int l= 2i; int r= 2i+1; while(lA[largest]) { largest=l; } while(rA[largest]) { largest=r; } if(largest!=i) { swap(A[largest], A[i]); heapify(A, n, largest); }} </pre> <hr></88,></p></55,></p></a[i])>