 #practiceLinkDiv { العرض: لا شيء! مهم؛ }
#practiceLinkDiv { العرض: لا شيء! مهم؛ }بالنظر إلى شجرة ثنائية، ابحث عن طول المسار الأطول الذي يتكون من عقد ذات قيم متتالية بترتيب متزايد. تعتبر كل عقدة بمثابة مسار بطول 1.
أمثلة:
In below diagram binary tree with longest consecutive path(LCP) are shown :
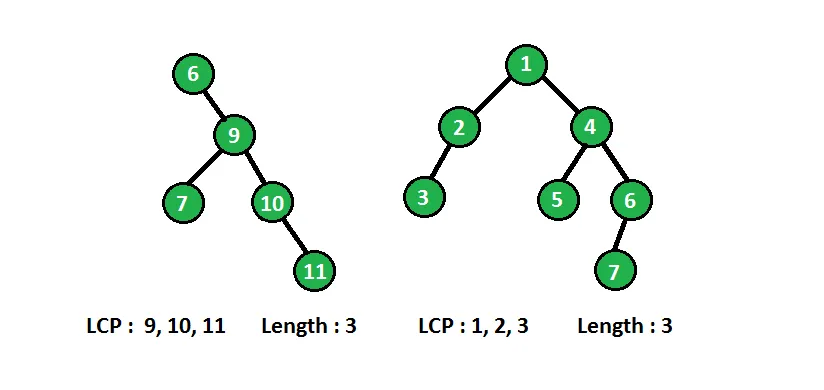
يمكننا حل المشكلة المذكورة أعلاه بشكل متكرر. في كل عقدة نحتاج إلى معلومات عن العقدة الأصلية الخاصة بها، إذا كانت العقدة الحالية لها قيمة واحدة أكثر من العقدة الأصلية، فإنها تقوم بإنشاء مسار متتالي في كل عقدة، وسنقارن قيمة العقدة بقيمتها الأصلية ونقوم بتحديث أطول مسار متتالي وفقًا لذلك.
للحصول على قيمة العقدة الأصلية، سنمرر (node_value + 1) كوسيطة للطريقة العودية ونقارن قيمة العقدة بقيمة الوسيطة هذه إذا استوفت تحديث الطول الحالي للمسار المتتالي وإلا قم بإعادة تهيئة طول المسار الحالي بمقدار 1.
يرجى الاطلاع على الكود أدناه لفهم أفضل:
C++// C/C++ program to find longest consecutive // sequence in binary tree #include
// Java program to find longest consecutive // sequence in binary tree class Node { int data; Node left right; Node(int item) { data = item; left = right = null; } } class Result { int res = 0; } class BinaryTree { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); System.out.println(tree.longestConsecutive(tree.root)); } } // This code is contributed by shubham96301
# Python3 program to find longest consecutive # sequence in binary tree # A utility class to create a node class newNode: def __init__(self data): self.data = data self.left = self.right = None # Utility method to return length of # longest consecutive sequence of tree def longestConsecutiveUtil(root curLength expected res): if (root == None): return # if root data has one more than its # parent then increase current length if (root.data == expected): curLength += 1 else: curLength = 1 # update the maximum by current length res[0] = max(res[0] curLength) # recursively call left and right subtree # with expected value 1 more than root data longestConsecutiveUtil(root.left curLength root.data + 1 res) longestConsecutiveUtil(root.right curLength root.data + 1 res) # method returns length of longest consecutive # sequence rooted at node root def longestConsecutive(root): if (root == None): return 0 res = [0] # call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res) return res[0] # Driver Code if __name__ == '__main__': root = newNode(6) root.right = newNode(9) root.right.left = newNode(7) root.right.right = newNode(10) root.right.right.right = newNode(11) print(longestConsecutive(root)) # This code is contributed by PranchalK
// C# program to find longest consecutive // sequence in binary tree using System; class Node { public int data; public Node left right; public Node(int item) { data = item; left = right = null; } } class Result { public int res = 0; } class GFG { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.Max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void Main(String []args) { GFG tree = new GFG(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); Console.WriteLine(tree.longestConsecutive(tree.root)); } } // This code is contributed by 29AjayKumar
<script> // JavaScript program to find longest consecutive // sequence in binary tree class Node { constructor(item) { this.data=item; this.left = this.right = null; } } let res = 0; let root; function longestConsecutive(root) { if (root == null) return 0; res=[0]; // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res[0]; } // Utility method to return length of longest // consecutive sequence of tree function longestConsecutiveUtil(rootcurlength expectedres) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res[0] = Math.max(res[0] curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code root = new Node(6); root.right = new Node(9); root.right.left = new Node(7); root.right.right = new Node(10); root.right.right.right = new Node(11); document.write(longestConsecutive(root)); // This code is contributed by rag2127 </script>
الإخراج
3
التعقيد الزمني: O(N) حيث N هو عدد العقد في شجرة ثنائية معينة.
المساحة المساعدة: O(log(N))
تمت مناقشته أيضًا على الرابط أدناه:
الحد الأقصى لطول المسار المتزايد المتتالي في الشجرة الثنائية
