يمكن استخدام شاشة العرض المكونة من سبعة أجزاء لعرض الأرقام. نظرا لمجموعة من ن الأعداد الطبيعية. وتتمثل المهمة في العثور على الرقم الموجود في المصفوفة الذي يستخدم الحد الأدنى لعدد المقاطع لعرض الرقم. إذا كانت الأرقام المتعددة تحتوي على الحد الأدنى لعدد المقاطع، فقم بإخراج الرقم الذي يحتوي على أصغر فهرس.
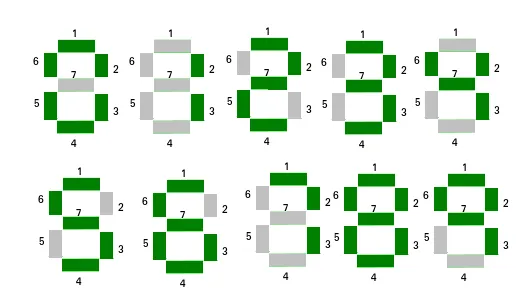
أمثلة :
مدخل : آر[] = { 1 2 3 4 5 }.
الإخراج : 1
توضيح: العنصر الذي يستخدم الحد الأدنى لعدد الشرائح هو 1 (أي 2 قطعة)مدخل : آر[] = { 489206745123756 }.
الإخراج : 745
توضيح: العنصر ذو الفهرس الأصغر الذي يستخدم الحد الأدنى لعدد الشرائح هو 745 (أي 12 قطعة)
تتمثل الفكرة في الحساب المسبق لعدد المقطع الذي تستخدمه الأرقام من 0 إلى 9 وتخزينه. الآن، لكل عنصر من عناصر المصفوفة، قم بجمع عدد المقاطع المستخدمة بواسطة كل رقم. ثم ابحث عن العنصر الذي يستخدم الحد الأدنى لعدد الأجزاء.
C++عدد القطعة المستخدمة بالرقم:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include
import java.io.*; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void main (String[] args) { int []arr = {489 206 745 123 756}; int n = arr.length; System.out.println(elementMinSegment(arr n)); } }
# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad
using System; class GFG{ // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void Main() { int []arr = {489 206 745 123 756}; int n = arr.Length; Console.WriteLine(elementMinSegment(arr n)); } }
// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) { if (x == 0) return seg[0]; let count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x = parseInt(x / 10 10); } return count; } function elementMinSegment(arr n) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment(arr[0]); let minindex = 0; // Finding and comparing segment used // by each number arr[i]. for(let i = 1; i < n; i++) { let temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));
الإخراج
745
تعقيد الوقت: O(n * log 10 ن)
المساحة المساعدة: O(10)
