ما هو المنحدر؟

عدد من القيم المطلقة التي تمثل ما إذا كان الخط أكثر حدة أو تملق و ال اتجاه من الخط على الرسم البياني المعروف باسم أ المنحدر أو التدرج. ميل الخط هو مفهوم أساسي في الاقتصاد والرياضيات. ويشار إليه عموما بالحرف 'م'. ويمكن حساب الميل عن طريق قسمة 'التغيير العمودي' مع ال 'التغيير الأفقي' بين نقطتين مختلفتين على الخط.

أنواع المنحدرات

هناك نوعان رئيسيان من المنحدرات الموضحة أدناه:

المنحدر الإيجابي:ميل يظهر فيه متغيران، أي المتغير عند المحور السيني والمتغير عند المحور الصادي، أ علاقة إيجابية معروف ب المنحدر الإيجابي. بكلمات أبسط، الميل الإيجابي هو الذي يزداد فيه المتغير x مع زيادة المتغير y و/أو المتغير y يزداد مع زيادة المتغير x. وبالمثل، فإن المتغير x يتناقص مع نقصان المتغير y، و/أو المتغير y يتناقص مع نقصان المتغير x. وهذا يعني أن كلا المتغيرين موجودان يكمل لبعضهم البعض. يتحرك منحدر إيجابي في الاتجاه التصاعدي أو هو منحدر للأعلى.
من الناحية الرسومية، الميل الإيجابي هو الذي يرتفع فيه الخط على الرسم البياني عندما يتحرك من اليسار إلى اليمين. يمكن فهم مفهوم المنحدر الإيجابي بوضوح بمساعدة منحنى العرض منتج أو شركة في مجال الاقتصاد. المتغيران في المنحنى هما السعر عند المحور y وكمية البضائع عند المحور x. لنفترض أن الشركة تنتج البضائع من أجلها تعظيم الربح. ولذلك، عندما ترتفع أسعار السلع، فإن الكمية التي تعرضها الشركة من تلك السلع سوف تزيد أيضا، بينما عندما تنخفض الأسعار، فإن الكمية التي تعرضها الشركة سوف تنخفض. وبعبارة أخرى، عند الأسعار المرتفعة، ستقوم الشركة أو المنتج بزيادة الكمية المعروضة لكسب المزيد من الأرباح، بينما عند الأسعار المنخفضة، سوف تقلل الكمية المعروضة لتقليل الخسارة. ومن ثم، فإنه يوضح أن الأسعار والكمية المعروضة ترتبط ارتباطا إيجابيا ببعضها البعض، وهو ما يمكن توضيحه من الرسم البياني أدناه:
المنحدر السلبي:ميل يظهر فيه متغيران، أي المتغير عند المحور السيني والمتغير عند المحور الصادي، أ علاقة سلبية معروف ب المنحدر السلبي. بمعنى آخر، الميل السلبي هو الذي يزداد فيه المتغير x مع نقصان المتغير y و/أو يزداد المتغير y مع نقصان المتغير x. وبنفس الطريقة، يتناقص المتغير x مع زيادة المتغير y، و/أو المتغير y يتناقص مع زيادة المتغير x. وهذا يمثل علاقة عكسية بين هذين المتغيرين. يتحرك منحدر سلبي في الاتجاه الهبوطي أو هو الهبوطي.
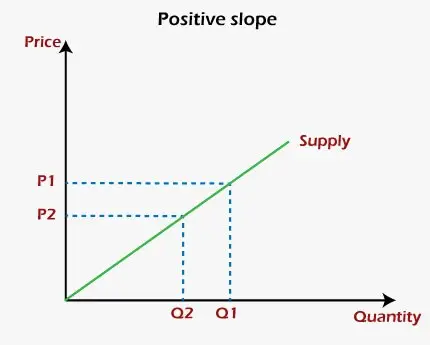
بيانيًا، الميل السلبي هو الذي يسقط فيه الخط على الرسم البياني عندما يتحرك من اليسار إلى اليمين. أحد أفضل الأمثلة على الميل السلبي للرسم البياني هو منحنى الطلب في الاقتصاد. المتغيران في المنحنى هما السعر عند المحور y وكمية البضائع عند المحور x. وكما نعلم، فإن المستهلكين يشترون كمية كبيرة من السلعة بسعر أقل من السعر الأعلى. ولذلك فإن الكمية التي يطلبها المستهلكون من السلع ستنخفض مع زيادة أسعار تلك السلع. ومن ناحية أخرى، عندما تنخفض أسعار السلع، فإن الطلب على الكمية سيزيد. وبالتالي يظهر أ علاقة سلبية بين الأسعار والكمية المعروضة من تلك السلع. ويمكن مسحه من الرسم البياني أدناه:

نوعان آخران من المنحدرات

بخلاف المنحدرات الإيجابية والسلبية، هناك نوعان آخران من المنحدرات تسمى المنحدر الصفري والمنحدر اللانهائي. ويمكن فهمها من التفسير المعطى:

المنحدر صفر:تُعرف الحالة التي يظل فيها المتغير عند المحور y كما هو مع التغير في المتغير عند المحور x باسم المنحدر من الصفر. بيانيا، أ خط أفقي أو مسطح على الرسم البياني له ميل صفر. ولذلك يطلق عليه أ وظيفة ثابتة. المنحدر من الصفر لا يتحرك في الاتجاه الصعودي أو الهبوطي. يتحرك فقط في اتجاه اليسار أو اليمين.
الرسم البياني أدناه هو عرض رسومي للمنحدر الصفري:
المنحدر اللانهائي:تُعرف الحالة التي يظل فيها المتغير عند المحور x كما هو مع التغيير في المتغير عند المحور y باسم المنحدر اللانهائي. ويسمى أيضا منحدر غير محدد وفقا للشروط الرسومية، أ خط عمودي أو عمودي على الرسم البياني له ميل لا نهاية له. المنحدر اللانهائي لا يتحرك إلى اليسار أو إلى اليمين. يظهر حركة فقط في الاتجاه الصعودي أو الهبوطي.
يظهر المنحدر اللانهائي في الرسم البياني الموضح:

حساب المنحدر

• في معادلة خطية الفأس + بواسطة + ج = 0، يتم تعريف المنحدر على أنه -أ/ب.
• يمكن حساب معادلة الخط بمساعدة صيغة نقطة المنحدر إذا كان كلا المنحدر م من خط ونقطة (×1، ص1) من المعروف. الصيغة موضحة أدناه:
  ص - y1 = م (س - x1)
• سيكون الخطين موازي إذا كانت المنحدرات الخاصة بهم متساوي، بينما سيكون سطرين عمودي إذا كان المنتج من منحدراتهم -1.

معلومات إضافية

• يتم استخدام القيمة المطلقة للميل لمعرفة ما إذا كان المنحنى موجودًا أم لا أكثر حدة أو تملق.
• القيمة الإيجابية والسلبية للمنحدر تحدد الاتجاه، أي لأعلى أو لأسفل، من المنحدر.
• يصبح منحنى أكثر انحدارا مع زيادة القيمة المطلقة للميل.
• يصبح منحنى بالاطراء مع انخفاض القيمة المطلقة للميل.
• هذه الشروط لا تتأثر المنحدر السلبي أو الإيجابي (وليس القيمة السلبية أو الإيجابية).
• أ انخفاض المنحدر الإيجابي يعني أنه سيتم تشكيل منحنى مسطح مائل في الاتجاه التصاعدي.
• أ منحدر إيجابي أعلى يعني أنه سيتم تشكيل منحنى أكثر انحدارًا منحنيًا في الاتجاه الصعودي.
• أ منحدر سلبي ذو قيمة مطلقة كبيرة يعني أنه سيتم تشكيل منحنى أكثر حدة يميل في الاتجاه الهبوطي.
• أ المنحدر السلبي له قيمة مطلقة أصغر يعني أنه سيتم تشكيل منحنى مسطح منحني في الاتجاه الهبوطي.