في هذه المقالة، سنناقش اجتياز الشجرة في بنية البيانات. مصطلح 'اجتياز الشجرة' يعني اجتياز أو زيارة كل عقدة من الشجرة. هناك طريقة واحدة لاجتياز بنية البيانات الخطية مثل القائمة المرتبطة وقائمة الانتظار والمكدس. حيث أن هناك طرق متعددة لاجتياز شجرة مدرجة على النحو التالي -

• اجتياز الطلب المسبق
• اجتياز غير النظام
• اجتياز الطلب البريدي

لذلك، في هذه المقالة، سنناقش التقنيات المذكورة أعلاه لاجتياز الشجرة. الآن، لنبدأ بمناقشة طرق اجتياز الأشجار.

اجتياز الطلب المسبق

تتبع هذه التقنية سياسة 'الجذر من اليسار إلى اليمين'. وهذا يعني أنه تتم زيارة العقدة الجذرية الأولى بعد اجتياز الشجرة الفرعية اليسرى بشكل متكرر، وأخيرًا، يتم اجتياز الشجرة الفرعية اليمنى بشكل متكرر. نظرًا لأنه يتم اجتياز العقدة الجذرية قبل (أو قبل) الشجرة الفرعية اليسرى واليمنى، فإن ذلك يسمى اجتياز الطلب المسبق.

لذلك، في اجتياز الطلب المسبق، تتم زيارة كل عقدة قبل كلتا الشجرتين الفرعيتين.

تشمل تطبيقات اجتياز الطلب المسبق -

• يتم استخدامه لإنشاء نسخة من الشجرة.
• يمكن استخدامه أيضًا للحصول على تعبير البادئة لشجرة التعبير.

خوارزمية

 Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively. 

مثال

الآن، دعونا نرى مثالاً على تقنية اجتياز الطلب المسبق.

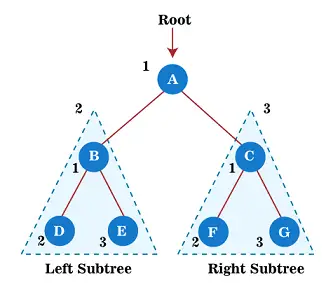
الآن، ابدأ بتطبيق اجتياز الطلب المسبق على الشجرة أعلاه. أولاً، نقوم باجتياز العقدة الجذرية أ؛ بعد ذلك، انتقل إلى الشجرة الفرعية اليسرى ب ، والتي سيتم أيضًا اجتيازها بالطلب المسبق.

لذلك، بالنسبة للشجرة الفرعية اليسرى B، أولاً، العقدة الجذرية ب يجتاز نفسه؛ بعد ذلك، الشجرة الفرعية اليسرى د يتم اجتيازها. منذ العقدة د ليس لديه أي أطفال، انتقل إلى الشجرة الفرعية اليمنى و . نظرًا لأن العقدة E أيضًا لا تحتوي على أي عناصر فرعية، فقد اكتمل اجتياز الشجرة الفرعية اليسرى للعقدة الجذرية A.

طرق القائمة جافا

انتقل الآن نحو الشجرة الفرعية اليمنى للعقدة الجذرية A والتي هي C. لذا، بالنسبة للشجرة الفرعية اليمنى C، أولًا العقدة الجذرية ج لقد اجتازت نفسها؛ بعد ذلك، الشجرة الفرعية اليسرى F يتم اجتيازها. منذ العقدة F ليس لديه أي أطفال، انتقل إلى الشجرة الفرعية الصحيحة ز . نظرًا لأن العقدة G لا تحتوي أيضًا على أي عناصر فرعية، فقد اكتمل اجتياز الشجرة الفرعية اليمنى للعقدة الجذرية A.

لذلك، يتم اجتياز جميع العقد في الشجرة. لذلك، فإن ناتج اجتياز الطلب المسبق للشجرة أعلاه هو -

أ → ب → د → ه → ج → و → ز

لمعرفة المزيد عن اجتياز الطلب المسبق في بنية البيانات، يمكنك اتباع الرابط اجتياز الطلب المسبق .

اجتياز الطلب البريدي

تتبع هذه التقنية سياسة 'الجذر من اليسار إلى اليمين'. وهذا يعني أنه تم اجتياز الشجرة الفرعية اليسرى الأولى من العقدة الجذرية، وبعد ذلك يتم اجتياز الشجرة الفرعية اليمنى بشكل متكرر، وأخيرًا، يتم اجتياز العقدة الجذرية. نظرًا لأنه يتم اجتياز العقدة الجذرية بعد (أو نشر) الشجرة الفرعية اليسرى واليمنى، فإن ذلك يسمى اجتياز الطلب اللاحق.

لذلك، في اجتياز ما بعد الطلب، تتم زيارة كل عقدة بعد كلتا الشجرتين الفرعيتين.

جافا الميراث

تشمل تطبيقات اجتياز ما بعد الطلب ما يلي -

• يتم استخدامه لحذف الشجرة.
• يمكن استخدامه أيضًا للحصول على تعبير postfix لشجرة التعبير.

خوارزمية

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node. 

مثال

الآن، دعونا نرى مثالاً على تقنية اجتياز ما بعد الطلب.

الآن، ابدأ بتطبيق اجتياز الطلب اللاحق على الشجرة أعلاه. أولاً، نجتاز الشجرة الفرعية اليسرى B التي سيتم اجتيازها في الترتيب اللاحق. بعد ذلك، سوف نجتاز الشجرة الفرعية الصحيحة ج في مرحلة ما بعد الطلب. وأخيرًا، العقدة الجذرية للشجرة المذكورة أعلاه، أي، أ ، يتم اجتيازه.

لينكس تغيير اسم الدليل

لذا، بالنسبة للشجرة الفرعية اليسرى B، أولًا، الشجرة الفرعية اليسرى د يتم اجتيازها. منذ العقدة د ليس لديه أي أطفال، قم باجتياز الشجرة الفرعية الصحيحة و . نظرًا لأن العقدة E أيضًا لا تحتوي على أي أطفال، فانتقل إلى العقدة الجذرية ب. بعد اجتياز العقدة ب، اكتمل اجتياز الشجرة الفرعية اليسرى للعقدة الجذرية A.

انتقل الآن نحو الشجرة الفرعية اليمنى للعقدة الجذرية A التي هي C. لذا، بالنسبة للشجرة الفرعية اليمنى C، أولًا الشجرة الفرعية اليسرى F يتم اجتيازها. منذ العقدة F ليس لديه أي أطفال، قم باجتياز الشجرة الفرعية الصحيحة ز . نظرًا لأن العقدة G أيضًا لا تحتوي على أي أطفال، وبالتالي، أخيرًا، العقدة الجذرية للشجرة الفرعية اليمنى، أي، ج، يتم اجتيازها. اكتمل اجتياز الشجرة الفرعية اليمنى للعقدة الجذرية A.

أخيرًا، قم باجتياز العقدة الجذرية لشجرة معينة، أي: أ . بعد اجتياز العقدة الجذرية، يكتمل اجتياز الترتيب اللاحق للشجرة المحددة.

لذلك، يتم اجتياز جميع العقد في الشجرة. لذلك، فإن ناتج اجتياز ما بعد الطلب للشجرة المذكورة أعلاه هو -

د → ه → ب → و → ز → ج → أ

لمعرفة المزيد عن اجتياز الطلب اللاحق في بنية البيانات، يمكنك اتباع الرابط اجتياز الطلب البريدي .

اجتياز غير النظام

تتبع هذه التقنية سياسة 'الجذر الأيسر واليمين'. وهذا يعني أنه تتم زيارة الشجرة الفرعية اليسرى الأولى بعد اجتياز العقدة الجذرية، وأخيرًا، يتم اجتياز الشجرة الفرعية اليمنى. نظرًا لأنه يتم اجتياز العقدة الجذرية بين الشجرة الفرعية اليمنى واليسرى، يطلق عليها اسم الاجتياز الداخلي.

لذلك، في الاجتياز الداخلي، تتم زيارة كل عقدة بين شجراتها الفرعية.

تتضمن تطبيقات اجتياز Inorder -

• يتم استخدامه للحصول على عقد BST بترتيب متزايد.
• يمكن استخدامه أيضًا للحصول على تعبير البادئة لشجرة التعبير.

خوارزمية

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively. 

مثال

الآن، دعونا نرى مثالاً على تقنية اجتياز Inorder.

الآن، ابدأ بتطبيق الاجتياز الداخلي على الشجرة أعلاه. أولاً، نجتاز الشجرة الفرعية اليسرى ب التي سيتم اجتيازها في الداخل. بعد ذلك، سوف نجتاز العقدة الجذرية أ . وأخيرًا، الشجرة الفرعية الصحيحة ج يتم اجتيازها بالترتيب.

لذلك، للشجرة الفرعية اليسرى ب أولاً، الشجرة الفرعية اليسرى د يتم اجتيازها. منذ العقدة د ليس لديه أي أطفال، لذلك بعد اجتيازه، عقدة ب سيتم اجتيازها، وأخيرًا، الشجرة الفرعية اليمنى للعقدة B، أي و ، يتم اجتيازه. العقدة E أيضًا ليس لديها أي أطفال؛ لذلك، اكتمل اجتياز الشجرة الفرعية اليسرى للعقدة الجذرية A.

بعد ذلك، قم باجتياز العقدة الجذرية لشجرة معينة، أي: أ .

أخيرًا، تحرك نحو الشجرة الفرعية اليمنى للعقدة الجذرية A التي هي C. لذا، بالنسبة للشجرة الفرعية اليمنى C؛ أولاً، الشجرة الفرعية اليسرى F يتم اجتيازها. منذ العقدة F ليس لديه أي أطفال، العقدة ج سيتم اجتيازها، وفي النهاية، الشجرة الفرعية اليمنى للعقدة C، أي، ز ، يتم اجتيازه. العقدة G أيضًا ليس لديها أي أطفال؛ لذلك، اكتمل اجتياز الشجرة الفرعية اليمنى للعقدة الجذرية A.

عندما يتم اجتياز جميع عقد الشجرة، يكتمل الاجتياز الداخلي للشجرة المحددة. ناتج الاجتياز الداخلي للشجرة أعلاه هو -

د → ب → ه → أ → و → ج → ز

لمعرفة المزيد عن اجتياز الترتيب الداخلي في بنية البيانات، يمكنك اتباع الرابط اجتياز غير النظام .

فوائد الانستقرام للاستخدام الشخصي

تعقيد تقنيات اجتياز الشجرة

التعقيد الزمني لتقنيات اجتياز الأشجار التي تمت مناقشتها أعلاه هو على) ، أين 'ن' هو حجم الشجرة الثنائية.

في حين أن التعقيد المكاني لتقنيات اجتياز الأشجار الذي تمت مناقشته أعلاه هو يا(1) إذا لم نأخذ في الاعتبار حجم المكدس لاستدعاءات الوظائف. خلاف ذلك، فإن التعقيد المكاني لهذه التقنيات أوه) ، أين 'ح' هو ارتفاع الشجرة.

تنفيذ اجتياز الشجرة

الآن، دعونا نرى تنفيذ التقنيات التي تمت مناقشتها أعلاه باستخدام لغات برمجة مختلفة.

برنامج: اكتب برنامجًا لتطبيق تقنيات اجتياز الأشجار في لغة C.

 #include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
 The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
 The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
 The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } 

انتاج |

برنامج: اكتب برنامجًا لتطبيق تقنيات اجتياز الشجرة في لغة C#.

 using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } 

انتاج |

برنامج: اكتب برنامجًا لتنفيذ تقنيات اجتياز الشجرة في لغة C++.

 #include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node-&gt;element = val; Node-&gt;left = NULL; Node-&gt;right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout&lt;<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root-&gt;left); cout&lt;<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root-&gt;right); cout&lt;<' '<element<left="createNode(28);" root->right = createNode(48); root-&gt;left-&gt;left = createNode(23); root-&gt;left-&gt;right = createNode(33); root-&gt;left-&gt;left-&gt;left = createNode(13); root-&gt;left-&gt;left-&gt;right = createNode(26); root-&gt;right-&gt;left = createNode(43); root-&gt;right-&gt;right = createNode(58); root-&gt;right-&gt;right-&gt;left = createNode(53); root-&gt;right-&gt;right-&gt;right = createNode(68); cout&lt;<'
 the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
 inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + &apos; &apos;); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + &apos; &apos;); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + &apos; &apos;); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println(&apos;The Preorder traversal of given binary tree is - &apos;); pt.traversePreorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Inorder traversal of given binary tree is - &apos;); pt.traverseInorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Postorder traversal of given binary tree is - &apos;); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that&apos;s all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'>

انتاج |

سانجاي دوت و

بعد تنفيذ الكود أعلاه سيكون الناتج -

خاتمة

في هذه المقالة، ناقشنا الأنواع المختلفة لتقنيات اجتياز الشجرة: اجتياز الطلب المسبق، واجتياز الطلب الداخلي، واجتياز ما بعد الطلب. لقد رأينا هذه التقنيات جنبًا إلى جنب مع الخوارزمية والمثال والتعقيد والتنفيذ في C وC++ وC# وJava.

لذلك، هذا كل ما في هذه المادة. نأمل أن تكون مفيدة وغنية بالمعلومات لك.