النسبة المئوية هي مفهوم أساسي في الرياضيات، وهي ليست مهمة في الرياضيات فحسب، بل مهمة أيضًا في حياتنا اليومية. فهو يساعدنا على التعبير عن الكسور والنسب ببساطة، مما يسهل مقارنة هذه القيم واستيعابها. أحد الأمثلة الشائعة التي تنشأ في العديد من السيناريوهات هو حساب 30 بالمائة، لذلك في هذه المقالة سوف نتعرف على مفهوم 30 بالمائة، ونفهم 30 بالمئة من 100، والتعرف على التطبيقات والخاتمة في النهاية.
فهم النسب المئوية
قبل أن نتعرف على حساب 30 بالمائة من 100، دعونا نتأكد من أن لدينا معرفة جيدة بمفهوم النسب المئوية. النسبة المئوية هي طريقة للتعبير عن نسبة أو جزء من 100. الرمز '%' يمثل نسبة مئوية ويتم قراءته كـ ' نسبه مئويه .' تُستخدم النسب المئوية بشكل شائع لمقارنة القيم وإصدار بيانات نسبية.
احسب 30% من 100
لحساب 30 بالمائة من 100، علينا اتباع عملية بسيطة. بما أن '30%' تعني 30 من 100، فيمكننا التعبير عنها في صورة كسر: 30/100. للعثور على 30% من 100، اضرب الكسر 30/100 في 100.
دعونا نقسم الحساب خطوة بخطوة
وسوف نتعلم كيفية حساب 30% من 100 بمساعدة بعض الخطوات البسيطة، والتي سيتم شرحها في السطور التالية.
باش إذا كان آخر
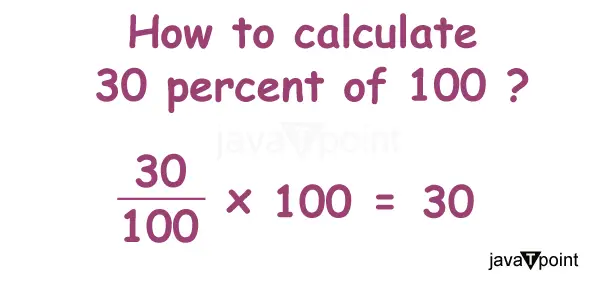
الخطوة 1 . أولاً، اكتب حاصل ضرب كلا الرقمين، أي 30% و100، كما هو موضح أدناه.
= 30% * 100
الخطوة 2 . وكما نعلم فإن معنى النسبة هو 100ذجزء من رقم أو أي شيء حتى نتمكن من استبدال '%' بـ (1/100).
= 30% * 100 = (30 / 100) * 100
الخطوه 3 . وباستخدام قواعد الضرب والتبسيط نحصل على ما يلي:
=30% * 100 = (30 / 100) * 100
= 3000 / 100
= 30
تطبيقات النسب المئوية
وفي المناقشة التالية، سوف نتعرف على بعض تطبيقات النسب المئوية المرتبطة بأمثلة من الحياة الواقعية.
1. خصومات التسوق: تخيل أنك قمت بزيارة متجر يقدم خصمًا بنسبة 30 بالمائة على منتج بقيمة 100 دولار. يجب عليك تحديد 30% من 100 دولار لحساب المبلغ الذي تدخره. باستخدام الحساب:
30 / 100 = 0.3
0.3 × 100 = 30
لذلك، ستوفر 30 دولارًا على العنصر الذي تبلغ قيمته 100 دولار؛ يجب عليك أن تدفع 70 دولارًا فقط.
2. درجات الامتحان: في إحدى المدارس، يحصل الطالب على 30 من 100 في اختبار الرياضيات. لتحديد النسبة المئوية لدرجات ذلك الطالب، نحتاج إلى حساب النسبة التي يمثلها 30 من أصل 100. باستخدام الصيغة:
30 / 100 = 0.3
0.3 × 100 = 30%
وبذلك حصل الطالب على 30% في اختبار الرياضيات.
3. أداء سوق الأوراق المالية: لنفترض أنك استثمرت 100 دولار في أحد الأسهم، وزاد السعر بنسبة 30 بالمائة. لحساب القيمة الجديدة لاستثمارك، عليك إيجاد 30 بالمائة من 100 دولار. باستخدام الطريقة الموضحة أعلاه:
30 / 100 = 0.3
0.3 × 100 = 30 دولارًا
يمكن أن يكون للفئة المجردة مُنشئ
زادت قيمة السهم بمقدار 30 دولارًا، مما يجعل قيمة استثمارك 130 دولارًا.
4. الاحتمالية: يتم استخدام النسب المئوية في حسابات الاحتمالية؛ إذا كان هناك احتمال بنسبة 35 بالمائة لهطول الأمطار اليوم، فهذا يعني أنه من بين كل 100 حالة جوية مماثلة، من المتوقع هطول الأمطار في 35 حالة.
5. التحليل الإحصائي: تُستخدم النسب المئوية على نطاق واسع في التحليل الإحصائي لتفسير البيانات؛ فهي تساعد في مقارنة النسب وحساب معدلات النمو وفهم التوزيعات.
بعض الأمثلة المحلولة
س: ما هي نسبة 30% من 10؟
حل:
الخطوة 1. 30% * 10
الخطوة 2. 30% * 10 = (30 / 100) * 10
الخطوة 3. 30% * 10 = (30 / 100) * 10 = 300 / 100 = 3
س: ما هي نسبة 30% من 50؟
حل:
الخطوة 1. 30% * 50
الخطوة 2. 30% * 50 = (30 / 100) * 50
الخطوة 3. 30% * 50 = (30 / 100) * 50 = 1500 / 100 = 15
س: ما هو 75% من 30؟
حل:
الخطوة 1. 75% * 30
الخطوة الثانية: 75% * 30 = (75 / 100) * 30
الخطوة 3. 75% * 30 = (75 / 100) * 30 = 2,250 / 100 = 22.5
س: ما هو 28% من 100؟
حل:
الخطوة 1. 28% * 100
الخطوة 2. 28% * 100 = (28 / 100) * 100
مجاني مقابل مجاني
الخطوة 3. 28% * 100 = (28 / 100) * 100 = 2800 / 100 = 28
س: ما هي نسبة 30% من 20؟
حل:
الخطوة 1. 30% * 20
الخطوة 2. 30% * 20 = (30 / 100) * 20
الخطوة 3. 30% * 20 = (30 / 100) * 20 = 600 / 100 = 6
س: ما هي نسبة 30% من 200؟
حل:
الخطوة 1. 30% * 200
الخطوة 2. 30% * 200 = (30 / 100) * 200
الخطوة 3. 30% * 200 = (30 / 100) * 200 = 6000 / 100 = 60
خاتمة
النسب المئوية هي مفهوم أساسي في الرياضيات يسمح لنا بالتعبير عن النسب وإجراء المقارنات. في حالتنا الخاصة بحساب 30% من 100، نضرب القيمة الإجمالية في 30% (0.3) للحصول على النتيجة، أي 30. هذه المعرفة سليمة في الرياضيات وقابلة للتطبيق في سيناريوهات مختلفة في العالم الحقيقي، مثل المبيعات والمكافآت. ، والاستثمارات المالية. ومن خلال فهم النسب المئوية والنسب، يمكننا تحسين قدراتنا على حل المشكلات واتخاذ قرارات مستنيرة في مختلف جوانب الحياة.
