أولا سوف نفهم شجرة ثنائية و شجرة البحث الثنائية بشكل منفصل، وبعد ذلك سننظر في الاختلافات بين الشجرة الثنائية وشجرة البحث الثنائية.

ما هي الشجرة الثنائية؟

أ شجرة ثنائية هوالمؤشر إلى الطفل الأيسر:يقوم بتخزين مرجع العقدة التابعة اليسرى.مؤشر للطفل المناسب:يقوم بتخزين مرجع العقدة التابعة اليمنى.عنصر البيانات:عنصر البيانات هو قيمة البيانات التي يتم تخزينها بواسطة العقدة.

يمكن تمثيل الشجرة الثنائية على النحو التالي:

جافا مقابل سي ++

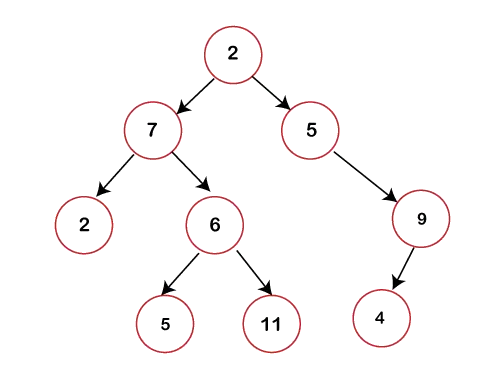
في الشكل أعلاه، يمكننا أن نلاحظ أن كل عقدة تحتوي على طفلين كحد أقصى. إذا كانت أي عقدة لا تحتوي على طفل يسار أو يمين، فإن قيمة المؤشر فيما يتعلق بهذا الطفل ستكون فارغة.

المصطلحات الأساسية المستخدمة في الشجرة الثنائية هي:

عقدة الجذر:العقدة الجذرية هي العقدة الأولى أو الأعلى في الشجرة الثنائية.عقدة الأم:عندما تكون العقدة متصلة بعقدة أخرى من خلال الحواف، تُعرف تلك العقدة بالعقدة الأصلية. في الشجرة الثنائية، يمكن أن تحتوي العقدة الأصلية على طفلين كحد أقصى.العقدة التابعة:إذا كانت العقدة لها سابقتها، فإن تلك العقدة تُعرف باسم a عقدة الطفل .عقدة ورقة:العقدة التي لا تحتوي على أي طفل تعرف باسم a عقدة ورقة .العقدة الداخلية:العقدة التي تحتوي على طفلين على الأقل تُعرف باسم العقدة الداخلية .عمق العقدة:تُعرف المسافة من العقدة الجذرية إلى العقدة المحددة بـ a عمق العقدة . نحن نقدم تسميات لجميع العقد مثل عقدة الجذر يتم تصنيفها بالرقم 0 لأنها لا تحتوي على عمق، ويتم تصنيف أبناء العقد الجذرية بالرقم 1، ويتم تصنيف أبناء العقد الجذرية بالرقم 2.ارتفاع:أطول مسافة من العقدة الجذرية إلى العقدة الورقية هي ارتفاع العقدة .

في الشجرة الثنائية، هناك شجرة واحدة تسمى شجرة ثنائية مثالية . إنها شجرة يجب أن تحتوي جميع العقد الداخلية فيها على عقدتين، ويجب أن تكون جميع العقد الورقية على نفس العمق. في حالة وجود شجرة ثنائية مثالية، يمكن حساب إجمالي عدد العقد الموجودة في الشجرة الثنائية باستخدام المعادلة التالية:

ن = 2^م+1-1

حيث n هو عدد العقد، وm هو عمق العقدة.

ما هي شجرة البحث الثنائية؟

أ شجرة البحث الثنائية هي شجرة تتبع ترتيبًا معينًا لترتيب العناصر، بينما الشجرة الثنائية لا تتبع أي ترتيب. في شجرة البحث الثنائية، يجب أن تكون قيمة العقدة اليسرى أصغر من العقدة الأصلية، ويجب أن تكون قيمة العقدة اليمنى أكبر من العقدة الأصلية.

دعونا نفهم مفهوم شجرة البحث الثنائية من خلال الأمثلة.

في الشكل أعلاه، يمكننا ملاحظة أن قيمة العقدة الجذرية هي 15، وهي أكبر من قيمة جميع العقد في الشجرة الفرعية اليسرى. قيمة العقدة الجذرية أقل من قيم جميع العقد في الشجرة الفرعية اليمنى. الآن، ننتقل إلى الطفل الأيسر للعقدة الجذرية. 10 أكبر من 8 وأقل من 12؛ كما أنها تلبي خاصية شجرة البحث الثنائية. الآن، ننتقل إلى الطفل الأيمن للعقدة الجذرية؛ القيمة 20 أكبر من 17 وأقل من 25؛ كما أنها تلبي خاصية شجرة البحث الثنائية. لذلك يمكننا القول أن الشجرة الموضحة أعلاه هي شجرة البحث الثنائية.

الآن، إذا قمنا بتغيير القيمة من 12 إلى 16 في الشجرة الثنائية أعلاه، فيجب علينا معرفة ما إذا كانت لا تزال شجرة بحث ثنائية أم لا.

جافا الرياضيات العشوائية

قيمة العقدة الجذرية هي 15 وهي أكبر من 10 ولكن أقل من 16، لذا فهي لا تلبي خاصية شجرة البحث الثنائية. لذلك، فهي ليست شجرة بحث ثنائية.

العمليات على شجرة البحث الثنائية

يمكننا إجراء عمليات الإدراج والحذف والبحث على شجرة البحث الثنائية. دعونا نفهم كيفية إجراء البحث في البحث الثنائي. تظهر الشجرة الثنائية أدناه والتي يتعين علينا إجراء عملية البحث عليها:

لنفترض أن علينا البحث عن 10 في الشجرة الثنائية أعلاه. لإجراء البحث الثنائي، سننظر في جميع الأعداد الصحيحة الموجودة في مصفوفة مرتبة. أولاً نقوم بإنشاء قائمة كاملة في مساحة البحث، وستكون كافة الأرقام موجودة في مساحة البحث. يتم تمييز مساحة البحث بمؤشرين، أي البداية والنهاية. يمكن تمثيل صفيف الشجرة الثنائية أعلاه على النحو التالي

أولاً، سنقوم بحساب العنصر الأوسط ومقارنة العنصر الأوسط بالعنصر المراد البحث عنه. يتم حساب العنصر الأوسط باستخدام n/2. قيمة n هي 7؛ وبالتالي فإن العنصر الأوسط هو 15. والعنصر الأوسط لا يساوي العنصر الذي تم البحث عنه، أي 10.

ملاحظة: إذا كان العنصر الذي يتم البحث عنه أقل من العنصر الأوسط، فسيتم إجراء البحث في النصف الأيسر؛ وإلا فسيتم البحث في النصف الأيمن. وفي حالة المساواة يوجد العنصر.

وبما أن العنصر المطلوب البحث عنه أقل من العنصر الأوسط، فسيتم إجراء البحث على المصفوفة اليسرى. الآن تم تقليل البحث إلى النصف، كما هو موضح أدناه:

العنصر الأوسط في المصفوفة اليسرى هو 10، وهو ما يساوي العنصر الذي تم البحث عنه.

تعقيد الوقت

في البحث الثنائي، هناك عناصر n. إذا كان العنصر الأوسط لا يساوي العنصر الذي تم البحث عنه، يتم تقليل مساحة البحث إلى n/2، وسنستمر في تقليل مساحة البحث بمقدار n/2 حتى يتم العثور على العنصر. في التخفيض بأكمله، إذا انتقلنا من n إلى n/2 إلى n/4 وما إلى ذلك، فسوف يستغرق الأمر log₂ن خطوات.

الاختلافات بين الشجرة الثنائية وشجرة البحث الثنائية