في هذه المقالة، سنناقش شجرة البحث الثنائية. ستكون هذه المقالة مفيدة جدًا وغنية بالمعلومات للطلاب ذوي الخلفية التقنية لأنها موضوع مهم في الدورة التدريبية.
قبل الانتقال مباشرة إلى شجرة البحث الثنائية، دعونا نرى أولاً وصفًا مختصرًا للشجرة.
ما هي الشجرة؟
الشجرة هي نوع من بنية البيانات المستخدمة لتمثيل البيانات في شكل هرمي. يمكن تعريفها على أنها مجموعة من الكائنات أو الكيانات التي تسمى بالعقد المرتبطة ببعضها البعض لمحاكاة التسلسل الهرمي. الشجرة عبارة عن بنية بيانات غير خطية حيث لا يتم تخزين البيانات الموجودة في الشجرة خطيًا أو تسلسليًا.
وظيفة النموذج C ++
الآن، لنبدأ بالموضوع، شجرة البحث الثنائي.
ما هي شجرة البحث الثنائية؟
تتبع شجرة البحث الثنائية بعض الترتيب لترتيب العناصر. في شجرة البحث الثنائية، يجب أن تكون قيمة العقدة اليسرى أصغر من العقدة الأصلية، ويجب أن تكون قيمة العقدة اليمنى أكبر من العقدة الأصلية. يتم تطبيق هذه القاعدة بشكل متكرر على الشجرتين الفرعيتين اليسرى واليمنى للجذر.
دعونا نفهم مفهوم شجرة البحث الثنائية مع مثال.
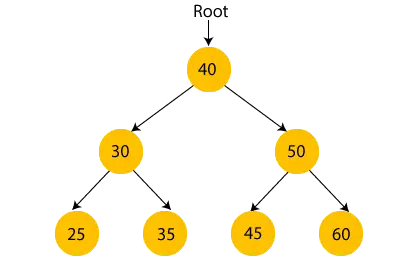
في الشكل أعلاه، يمكننا ملاحظة أن عقدة الجذر هي 40، وجميع عقد الشجرة الفرعية اليسرى أصغر من عقدة الجذر، وجميع عقد الشجرة الفرعية اليمنى أكبر من عقدة الجذر.
وبالمثل، يمكننا أن نرى أن الطفل الأيسر للعقدة الجذرية أكبر من الطفل الأيسر وأصغر من الطفل الأيمن. لذلك، فهو يفي أيضًا بخاصية شجرة البحث الثنائية. لذلك يمكننا القول أن الشجرة الموجودة في الصورة أعلاه هي شجرة بحث ثنائية.
لنفترض أننا إذا قمنا بتغيير قيمة العقدة 35 إلى 55 في الشجرة أعلاه، فتحقق مما إذا كانت الشجرة ستكون شجرة بحث ثنائية أم لا.

في الشجرة أعلاه، قيمة العقدة الجذرية هي 40، وهي أكبر من الابن الأيسر 30 ولكنها أصغر من الابن الأيمن 30، أي 55. لذا، فإن الشجرة أعلاه لا تفي بخاصية شجرة البحث الثنائية. ولذلك، فإن الشجرة المذكورة أعلاه ليست شجرة بحث ثنائية.
مزايا شجرة البحث الثنائية
- يعد البحث عن عنصر في شجرة البحث الثنائية أمرًا سهلاً حيث لدينا دائمًا تلميح حول الشجرة الفرعية التي تحتوي على العنصر المطلوب.
- بالمقارنة مع المصفوفات والقوائم المرتبطة، تكون عمليات الإدراج والحذف أسرع في BST.
مثال على إنشاء شجرة بحث ثنائية
الآن، دعونا نرى إنشاء شجرة بحث ثنائية باستخدام مثال.
لنفترض أن عناصر البيانات - 45، 15، 79، 90، 10، 55، 12، 20، 50
- أولا، علينا أن ندخل أربعة خمسة في الشجرة كجذر الشجرة.
- ثم اقرأ العنصر التالي؛ إذا كان أصغر من العقدة الجذرية، فأدخله كجذر للشجرة الفرعية اليسرى، وانتقل إلى العنصر التالي.
- بخلاف ذلك، إذا كان العنصر أكبر من العقدة الجذرية، فقم بإدراجه كجذر للشجرة الفرعية اليمنى.
الآن، دعونا نرى عملية إنشاء شجرة البحث الثنائية باستخدام عنصر البيانات المحدد. تظهر عملية إنشاء BST أدناه -
الخطوة 1 - أدخل 45.

الخطوة 2 - أدخل 15.
نظرًا لأن 15 أصغر من 45، فقم بإدراجه كعقدة جذر للشجرة الفرعية اليسرى.

الخطوة 3 - أدخل 79.
نظرًا لأن 79 أكبر من 45، فقم بإدراجه باعتباره العقدة الجذرية للشجرة الفرعية اليمنى.

الخطوة 4 - أدخل 90.
90 أكبر من 45 و79، لذلك سيتم إدراجها كالشجرة الفرعية اليمنى للرقم 79.

الخطوة 5 - أدخل 10.
10 أصغر من 45 و15، لذا سيتم إدراجه كشجرة فرعية يسرى مكونة من 15.

الخطوة 6 - أدخل 55.
55 أكبر من 45 وأصغر من 79، لذلك سيتم إدراجها كالشجرة الفرعية اليسرى لـ 79.

الخطوة 7 - أدخل 12.
12 أصغر من 45 و15 ولكنه أكبر من 10، لذا سيتم إدراجه كشجرة فرعية صحيحة مكونة من 10.

الخطوة 8 - أدخل 20.
20 أصغر من 45 ولكنه أكبر من 15، لذلك سيتم إدراجها كشجرة فرعية صحيحة مكونة من 15.

الخطوة 9 - أدخل 50.
50 أكبر من 45 ولكنه أصغر من 79 و55. لذا، سيتم إدراجها كشجرة فرعية يسرى مكونة من 55.

الآن، تم الانتهاء من إنشاء شجرة البحث الثنائية. بعد ذلك، دعونا ننتقل نحو العمليات التي يمكن إجراؤها على شجرة البحث الثنائية.
يمكننا إجراء عمليات الإدراج والحذف والبحث على شجرة البحث الثنائية.
دعونا نفهم كيفية إجراء البحث على شجرة البحث الثنائية.
البحث في شجرة البحث الثنائية
البحث يعني العثور على عنصر أو عقدة معينة أو تحديد موقعها في بنية البيانات. في شجرة البحث الثنائية، يكون البحث عن عقدة أمرًا سهلاً لأن العناصر في BST يتم تخزينها بترتيب معين. يتم سرد خطوات البحث عن عقدة في شجرة البحث الثنائية على النحو التالي -
- أولاً، قم بمقارنة العنصر المطلوب البحث عنه مع العنصر الجذري للشجرة.
- إذا كان الجذر مطابقًا للعنصر الهدف، فقم بإرجاع موقع العقدة.
- إذا لم يكن مطابقًا، فتحقق مما إذا كان العنصر أقل من العنصر الجذر، وإذا كان أصغر من العنصر الجذر، فانتقل إلى الشجرة الفرعية اليسرى.
- إذا كان أكبر من العنصر الجذر، فانتقل إلى الشجرة الفرعية اليمنى.
- كرر الإجراء أعلاه بشكل متكرر حتى يتم العثور على التطابق.
- إذا لم يتم العثور على العنصر أو أنه غير موجود في الشجرة، فسيتم إرجاع NULL.
الآن دعونا نفهم البحث في الشجرة الثنائية باستخدام مثال. نحن نأخذ شجرة البحث الثنائية التي تم تشكيلها أعلاه. لنفترض أنه يتعين علينا العثور على العقدة 20 من الشجرة أدناه.
الخطوة 1:

الخطوة 2:

الخطوه 3:

الآن، دعونا نرى الخوارزمية للبحث عن عنصر في شجرة البحث الثنائية.
خوارزمية للبحث عن عنصر في شجرة البحث الثنائية
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> انتاج |
بعد تنفيذ الكود أعلاه سيكون الناتج -
كود هوفمان الترميز

لذلك، هذا كل ما في هذه المادة. نأمل أن تكون المقالة مفيدة وغنية بالمعلومات لك.
