يُستخدم الالتواء في العديد من الأشياء مثل حساب المشتقات واكتشاف الحواف وتطبيق التمويه وما إلى ذلك، ويتم كل ذلك باستخدام 'نواة الالتواء'. النواة التلافيفية هي مصفوفة صغيرة جدًا وفي هذه المصفوفة، تحتوي كل خلية على رقم وأيضًا نقطة ربط.
تُستخدم نقطة الربط لمعرفة موضع النواة بالنسبة للصورة. يبدأ من الزاوية العلوية اليسرى من الصورة ويتحرك على كل بكسل بالتسلسل. يتداخل Kernel مع عدد قليل من وحدات البكسل في كل موضع من الصورة. يتم مضاعفة كل بكسل متداخل ثم إضافته. ويتم تعيين المبلغ كقيمة الموقف الحالي.
يساوي الطريقة في جافا
الالتفاف هو العملية التي تتم فيها إضافة كل عنصر من عناصر الصورة إلى جيرانه المحليين، ثم يتم وزنه بواسطة النواة. إنه مرتبط بشكل من أشكال الإلتواء الرياضي.
في عملية الالتواء، لا تقوم المصفوفة بعملية ضرب المصفوفات التقليدية ولكن يُشار إليها بالرمز *.
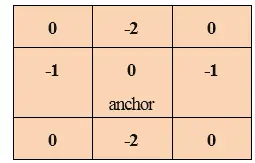
لنفترض أن هناك مصفوفتين 3x3، إحداهما عبارة عن نواة والأخرى عبارة عن قطعة صورة. في عملية الالتفاف، يتم قلب صفوف وأعمدة النواة ثم يتم ضربها ثم يتم إجراء الجمع. العناصر الموجودة في وسط المصفوفة، أي في [2،2] من الصورة، ستكون مزيجًا مرجحًا من مصفوفة الصورة وسيتم إعطاء الأوزان بواسطة النواة. وبالمثل، سيتم ترجيح جميع العناصر الأخرى للمصفوفة ثم يتم حساب الأوزان.
فيما يلي رمز زائف لوصف عملية الالتواء:
طريقة السلسلة الفرعية في جافا
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
يمكن حساب الالتواء باستخدام حلقات for المتعددة. لكن استخدام حلقات for يؤدي إلى الكثير من العمليات الحسابية المتكررة ويؤدي أيضًا إلى زيادة حجم الصورة والنواة. باستخدام تقنية تحويل فورييه المنفصلة، يمكن إجراء حساب الإلتواء بسرعة. في هذه التقنية، يتم تحويل عملية الالتواء بأكملها إلى عملية ضرب بسيطة.
في الالتفاف، تحدث المشكلة عندما تكون النواة بالقرب من الحافة أو الزوايا لأن النواة ثنائية الأبعاد.
وللتغلب على هذه المشاكل يمكن القيام بالأمور التالية:
- يمكن تجاهل تلك
- يمكن إنشاء وحدات بكسل إضافية بالقرب من الحواف.
يمكن إنشاء وحدات بكسل إضافية بالطرق التالية:
- بكسل حافة مكررة.
- تعكس الحواف
- يمكن نسخ البكسل من الطرف الآخر.
