مثال 1:
قم بتصميم NFA لجدول الانتقال كما هو موضح أدناه:
| الحالة الحالية | 0 | 1 |
|---|---|---|
| →س0 | س0، س1 | س0، س2 |
| س1 | س3 | ه |
| q2 | q2, q3 | س3 |
| →س3 | س3 | س3 |
حل:
يمكن رسم مخطط الانتقال باستخدام وظيفة التعيين كما هو موضح في الجدول.
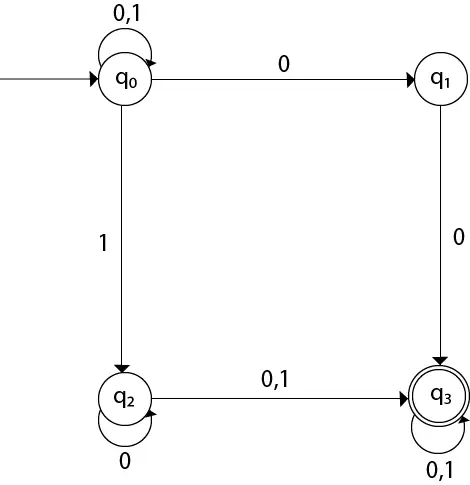
هنا،
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} مثال 2:
تصميم NFA مع ∑ = {0, 1} يقبل كل السلسلة التي تنتهي بـ 01.
math.random جافا
حل:

ومن ثم فإن NFA سيكون:

مثال 3:
صمم NFA بـ ∑ = {0, 1} حيث يكون '1' مزدوجًا متبوعًا بـ '0' مزدوجًا.
حل:
التفاف الكلمات CSS
اتحاد كرة القدم مع مزدوج 1 هو كما يلي:

يجب أن يتبعه مباشرة 0 مزدوج.
ثم،

الآن قبل مضاعفة 1، يمكن أن يكون هناك أي سلسلة من 0 و1. وبالمثل، بعد 0 مزدوج، يمكن أن يكون هناك أي سلسلة من 0 و1.
وبالتالي يصبح NFA:
bfs مقابل dfs

الآن النظر في السلسلة 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
مثال 4:
صمم NFA حيث تحتوي كل السلسلة على سلسلة فرعية 1110.
حل:
تتكون اللغة من كل السلسلة التي تحتوي على السلسلة الفرعية 1010. يمكن أن يكون مخطط الانتقال الجزئي:

الآن، يمكن أن يكون 1010 هو السلسلة الفرعية. ومن ثم سنضيف المدخلات 0 و1 بحيث يمكن الحفاظ على السلسلة الفرعية 1010 للغة. وبالتالي يصبح NFA:
ما هو الهاشتاج في جافا

يمكن إعطاء الجدول الانتقالي لمخطط الانتقال أعلاه أدناه:
| الحالة الحالية | 0 | 1 |
|---|---|---|
| →س1 | س1 | q1, q2 |
| q2 | س3 | |
| س3 | س4 | |
| س4 | س5 | *س5 | س5 | س5 |
النظر في سلسلة 111010،
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
لقد علقت! نظرًا لعدم وجود مسار من q2 لرمز الإدخال 0. يمكننا معالجة السلسلة 111010 بطريقة أخرى.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
كحالة q5 هي حالة القبول. لقد حصلنا على الفحص الكامل، ووصلنا إلى الحالة النهائية.
مثال 5:
تصميم NFA مع ∑ = {0, 1} يقبل كل السلسلة التي يكون فيها الرمز الثالث من الطرف الأيمن دائمًا 0.
كيفية حذف العمود في postgresql
حل:

وهكذا نحصل على الرمز الثالث من الطرف الأيمن بالرمز '0' دائمًا. يمكن أن يكون NFA:

الصورة أعلاه هي NFA لأنه في الحالة q0 مع الإدخال 0، يمكننا إما الانتقال إلى الحالة q0 أو q1.
