يشير التجميع الهرمي إلى إجراء تعليمي غير خاضع للرقابة يحدد مجموعات متتالية بناءً على مجموعات محددة مسبقًا. إنه يعمل من خلال تجميع البيانات في شجرة من المجموعات. إحصائيات التجميع الهرمية من خلال التعامل مع كل نقاط البيانات كمجموعة فردية. تشير نقطة النهاية إلى مجموعة مختلفة من المجموعات، حيث تختلف كل مجموعة عن المجموعة الأخرى، وتكون الكائنات داخل كل مجموعة متماثلة مع بعضها البعض.

نوع كومة

هناك نوعان من المجموعات الهرمية

• التكتل الهرمي التكتل
• التجمعات التقسيمية

التجمعات الهرمية التكتلية

يعد التجميع التكتل أحد أكثر أنواع التجميع الهرمي شيوعًا المستخدمة لتجميع الكائنات المتشابهة في مجموعات. يُعرف التجميع التكتل أيضًا باسم AGNES (التداخل التكتل). في التجميع التجميعي، تعمل كل نقطة بيانات كمجموعة فردية وفي كل خطوة، يتم تجميع كائنات البيانات بطريقة تصاعدية. في البداية، يكون كل كائن بيانات موجودًا في مجموعته. في كل تكرار، يتم دمج المجموعات مع مجموعات مختلفة حتى يتم تشكيل مجموعة واحدة.

خوارزمية التجميع الهرمي التكتلية

1. تحديد التشابه بين الأفراد وجميع المجموعات الأخرى. (ابحث عن مصفوفة القرب).
2. النظر في كل نقطة بيانات كمجموعة فردية.
3. الجمع بين مجموعات مماثلة.
4. إعادة حساب مصفوفة القرب لكل مجموعة.
5. كرر الخطوة 3 والخطوة 4 حتى تحصل على مجموعة واحدة.

دعونا نفهم هذا المفهوم بمساعدة التمثيل الرسومي باستخدام مخطط الأشجار.

بمساعدة العرض التوضيحي المعطى، يمكننا أن نفهم كيفية عمل الخوارزمية الفعلية. هنا لم يتم إجراء أي حساب دون افتراض القرب بين المجموعات.

لنفترض أن لدينا ست نقاط بيانات مختلفة P، Q، R، S، T، V.

سلسلة من الصفيف في ج

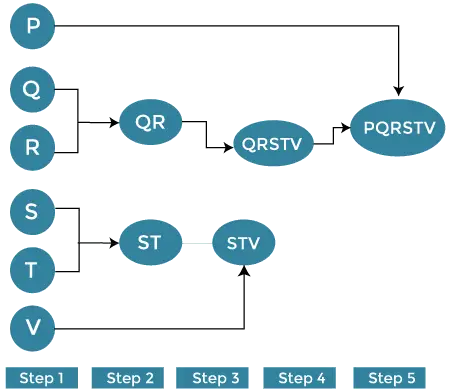
الخطوة 1:

اعتبر كل أبجدية (P، Q، R، S، T، V) بمثابة مجموعة فردية وأوجد المسافة بين المجموعة الفردية وجميع المجموعات الأخرى.

math.random جافا

الخطوة 2:

الآن، قم بدمج المجموعات المماثلة في مجموعة واحدة. لنفترض أن المجموعة Q والمجموعة R متشابهتان مع بعضهما البعض حتى نتمكن من دمجهما في الخطوة الثانية. وأخيرا، نحصل على المجموعات [ (P)، (QR)، (ST)، (V)]

الخطوه 3:

هنا، نقوم بإعادة حساب القرب وفقًا للخوارزمية ونجمع بين أقرب مجموعتين [(ST)، (V)] معًا لتشكيل مجموعات جديدة مثل [(P)، (QR)، (STV)]

الخطوة 4:

برامج جافا عينة

كرر نفس العملية. المجموعتان STV وPQ قابلة للمقارنة ويتم دمجهما معًا لتكوين مجموعة جديدة. الآن لدينا [(P)، (QQRSTV)].

الخطوة 5:

وأخيرا، يتم دمج المجموعتين المتبقيتين معا لتشكيل مجموعة واحدة [(PQRSTV)]

تقسيم التسلسل الهرمي

التجمع الهرمي المقسم هو عكس التجمع الهرمي التكتلي تمامًا. في التجميع الهرمي المقسم، تعتبر جميع نقاط البيانات مجموعة فردية، وفي كل تكرار، يتم فصل نقاط البيانات غير المتشابهة عن المجموعة. يتم التعامل مع نقاط البيانات المنفصلة كمجموعة فردية. أخيرًا، يتبقى لدينا مجموعات N.

مزايا التجميع الهرمي

• إنه سهل التنفيذ ويعطي أفضل النتائج في بعض الحالات.
• إنه سهل وينتج عنه تسلسل هرمي، وهو هيكل يحتوي على مزيد من المعلومات.
• لا يحتاج منا أن نحدد مسبقًا عدد المجموعات.

مساوئ التجميع الهرمي

• إنه يكسر التجمعات الكبيرة.
• من الصعب التعامل مع مجموعات مختلفة الحجم وأشكال محدبة.
• إنه حساس للضوضاء والقيم المتطرفة.
• لا يمكن أبدًا تغيير الخوارزمية أو حذفها بمجرد القيام بذلك مسبقًا.