لقد رأينا طرقًا مختلفة ذات تعقيدات زمنية مختلفة لحساب LCA في شجرة n-ary: -
الطريقة 1 : الطريقة الساذجة (عن طريق حساب مسار الجذر إلى العقدة) | O(n) لكل استعلام
الطريقة الثانية : باستخدام التحلل Sqrt | يا (جذر ح)
الطريقة الثالثة : استخدام نهج Spase Matrix DP | يا (تسجيل الدخول)
دعونا ندرس طريقة أخرى ذات وقت استعلام أسرع من جميع الطرق المذكورة أعلاه. لذلك سيكون هدفنا هو حساب LCA وقت ثابت ~ O(1) . دعونا نرى كيف يمكننا تحقيق ذلك.
الطريقة الرابعة: استخدام الحد الأدنى للاستعلام عن النطاق
لقد ناقشنا LCA وRMQ للشجرة الثنائية . نناقش هنا مشكلة LCA لتحويل مشكلة RMQ لشجرة n-ary.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
المفهوم الرئيسي : في هذه الطريقة، سنقوم بتقليل مشكلة LCA إلى مشكلة RMQ (الحد الأدنى لاستعلام النطاق) عبر مصفوفة ثابتة. بمجرد القيام بذلك، سنقوم بربط استعلامات الحد الأدنى للنطاق باستعلامات LCA المطلوبة.
ستكون الخطوة الأولى هي تحليل الشجرة إلى مصفوفة خطية مسطحة. للقيام بذلك يمكننا تطبيق مسيرة أويلر. سيعطي مسار أويلر اجتياز الرسم البياني مسبقًا. لذلك سنقوم بإجراء جولة أويلر على الشجرة وتخزين العقد في مصفوفة أثناء زيارتنا لها. هذه العملية تقلل الشجرة > 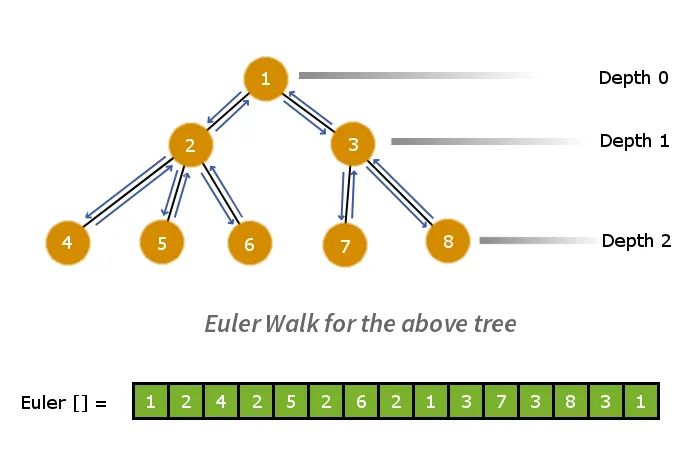
الآن دعونا نفكر بشكل عام: فكر في أي عقدتين على الشجرة. سيكون هناك مسار واحد بالضبط يربط بين العقدتين وستكون العقدة التي لها أصغر قيمة عمق في المسار هي LCA للعقدتين المحددتين.
الآن خذ أي عقدتين متميزتين على سبيل المثال في و ضد في مصفوفة سير أويلر. الآن جميع العناصر الموجودة في المسار من u إلى v سوف تقع بين فهرس العقدتين u و v في مصفوفة Euler walk. لذلك نحتاج فقط إلى حساب العقدة ذات الحد الأدنى من العمق بين فهرس العقدة u والعقدة v في مصفوفة أويلر.
لهذا سنحتفظ بمصفوفة أخرى تحتوي على عمق جميع العقد المقابلة لموضعها في مصفوفة Euler walk حتى نتمكن من تطبيق خوارزمية RMQ عليها.
فيما يلي مصفوفة سير أويلر الموازية لمصفوفة مسار العمق الخاصة بها.

الماسح الضوئي التالي جافا
مثال:- فكر في عقدتين العقدة 6 و العقدة 7 في مصفوفة أويلر. لحساب LCA للعقدة 6 والعقدة 7، فإننا ننظر إلى أصغر قيمة عمق لجميع العقد الموجودة بين العقدة 6 والعقدة 7.
لذلك العقدة 1 لديه الأصغر قيمة العمق = 0 ومن ثم فهو LCA للعقدة 6 والعقدة 7.

تطبيق:-
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
مسار أويلر ومصفوفة العمق هما نفس ما هو موضح أعلاه
فهرس المظهر الأول FAI[] : ستقوم مصفوفة فهرس المظهر الأول بتخزين فهرس الموضع الأول لكل عقدة في مصفوفة مسار أويلر. FAI[i] = أول ظهور للعقدة i في مصفوفة Euler Walk.
ويرد أدناه تنفيذ الطريقة المذكورة أعلاه: -
تطبيق:
C++// C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std; #define sz 101 vector < int > adj[sz]; // stores the tree vector < int > euler; // tracks the eulerwalk vector < int > depthArr; // depth for each node corresponding // to eulerwalk int FAI[sz]; // stores first appearance index of every node int level[sz]; // stores depth for all nodes in the tree int ptr; // pointer to euler walk int dp[sz][18]; // sparse table int logn[sz]; // stores log values int p2[20]; // stores power of 2 void buildSparseTable(int n) { // initializing sparse table memset(dp-1sizeof(dp)); // filling base case values for (int i=1; i<n; i++) dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i; // dp to fill sparse table for (int l=1; l<15; l++) for (int i=0; i<n; i++) if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1) dp[i][l] = (depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])? dp[i+p2[l-1]][l-1] : dp[i][l-1]; else break; } int query(int lint r) { int d = r-l; int dx = logn[d]; if (l==r) return l; if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]) return dp[r-p2[dx]][dx]; else return dp[l][dx]; } void preprocess() { // memorizing powers of 2 p2[0] = 1; for (int i=1; i<18; i++) p2[i] = p2[i-1]*2; // memorizing all log(n) values int val = 1ptr=0; for (int i=1; i<sz; i++) { logn[i] = ptr-1; if (val==i) { val*=2; logn[i] = ptr; ptr++; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs(int curint prevint dep) { // marking FAI for cur node if (FAI[cur]==-1) FAI[cur] = ptr; level[cur] = dep; // pushing root to euler walk euler.push_back(cur); // incrementing euler walk pointer ptr++; for (auto x:adj[cur]) { if (x != prev) { dfs(xcurdep+1); // pushing cur again in backtrack // of euler walk euler.push_back(cur); // increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr() { for (auto x : euler) depthArr.push_back(level[x]); } int LCA(int uint v) { // trivial case if (u==v) return u; if (FAI[u] > FAI[v]) swap(uv); // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } void addEdge(int uint v) { adj[u].push_back(v); adj[v].push_back(u); } int main(int argc char const *argv[]) { // constructing the described tree int numberOfNodes = 8; addEdge(12); addEdge(13); addEdge(24); addEdge(25); addEdge(26); addEdge(37); addEdge(38); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; memset(FAI-1sizeof(FAI)); dfs(100); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.size()); cout << 'LCA(67) : ' << LCA(67) << 'n'; cout << 'LCA(64) : ' << LCA(64) << 'n'; return 0; }
// Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList; import java.util.Arrays; class GFG{ static int sz = 101; @SuppressWarnings('unchecked') // Stores the tree static ArrayList<Integer>[] adj = new ArrayList[sz]; // Tracks the eulerwalk static ArrayList<Integer> euler = new ArrayList<>(); // Depth for each node corresponding static ArrayList<Integer> depthArr = new ArrayList<>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[][] dp = new int[sz][18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[i][j] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 1][0] = (depthArr.get(i) > depthArr.get(i - 1)) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[i][l - 1] != -1 && dp[i + p2[l - 1]][l - 1] != -1) dp[i][l] = (depthArr.get(dp[i][l - 1]) > depthArr.get( dp[i + p2[l - 1]][l - 1])) ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr.get(dp[l][dx]) > depthArr.get(dp[r - p2[dx]][dx])) return dp[r - p2[dx]][dx]; else return dp[l][dx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.add(cur); // Incrementing euler walk pointer ptr++; for(Integer x : adj[cur]) { if (x != prev) { dfs(x cur dep + 1); // Pushing cur again in backtrack // of euler walk euler.add(cur); // Increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { for(Integer x : euler) depthArr.add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler.get(query(FAI[u] FAI[v])); } static void addEdge(int u int v) { adj[u].add(v); adj[v].add(u); } // Driver code public static void main(String[] args) { for(int i = 0; i < sz; i++) { adj[i] = new ArrayList<>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Arrays.fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.size()); System.out.println('LCA(67) : ' + LCA(6 7)); System.out.println('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by sanjeev2552
# Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range(101)] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [-1] * 101 # stores depth for all nodes in the tree level = [0] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[-1] * 18 for _ in range(101)] # stores log values logn = [0] * 101 # stores power of 2 p2 = [0] * 20 def buildSparseTable(n: int): # initializing sparse table for i in range(n): dp[i][0] = i-1 if depthArr[i] > depthArr[i-1] else i # dp to fill sparse table for l in range(1 15): for i in range(n): if dp[i][l-1] != -1 and dp[i+p2[l-1]][l-1] != -1: dp[i][l] = dp[i+p2[l-1]][l-1] if depthArr[dp[i][l-1] ] > depthArr[dp[i+p2[l-1]][l-1]] else dp[i][l-1] else: break def query(l: int r: int) -> int: d = r-l dx = logn[d] if l == r: return l if depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]: return dp[r-p2[dx]][dx] else: return dp[l][dx] def preprocess(): global ptr # memorizing powers of 2 p2[0] = 1 for i in range(1 18): p2[i] = p2[i-1]*2 # memorizing all log(n) values val = 1 ptr = 0 for i in range(1 101): logn[i] = ptr-1 if val == i: val *= 2 logn[i] = ptr ptr += 1 def dfs(cur: int prev: int dep: int): global ptr # marking FAI for cur node if FAI[cur] == -1: FAI[cur] = ptr level[cur] = dep # pushing root to euler walk euler.append(cur) # incrementing euler walk pointer ptr += 1 for x in adj[cur]: if x != prev: dfs(x cur dep+1) # pushing cur again in backtrack # of euler walk euler.append(cur) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr(): global depthArr for x in euler: depthArr.append(level[x]) def LCA(u: int v: int) -> int: # trivial case if u == v: return u if FAI[u] > FAI[v]: u v = v u # doing RMQ in the required range return euler[query(FAI[u] FAI[v])] def addEdge(u v): adj[u].append(v) adj[v].append(u) # constructing the described tree numberOfNodes = 8 addEdge(1 2) addEdge(1 3) addEdge(2 4) addEdge(2 5) addEdge(2 6) addEdge(3 7) addEdge(3 8) # performing required precalculations preprocess() # doing the Euler walk ptr = 0 FAI = [-1] * (numberOfNodes + 1) dfs(1 0 0) # creating depthArray corresponding to euler[] makeArr() # building sparse table buildSparseTable(len(depthArr)) print('LCA(67) : ' LCA(6 7)) print('LCA(64) : ' LCA(6 4))
// C# program to demonstrate LCA of n-ary // tree in constant time. using System; using System.Collections.Generic; public class GFG { static int sz = 101; // Stores the tree static List<int>[] adj = new List<int>[sz]; // Tracks the eulerwalk static List<int> euler = new List<int>(); // Depth for each node corresponding static List<int> depthArr = new List<int>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[] dp = new int[sz 18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[ij] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 10] = (depthArr[i] > depthArr[i - 1]) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[il - 1] != -1 && dp[i + p2[l - 1]l - 1] != -1) dp[il] = (depthArr[dp[il - 1]] > depthArr[dp[i + p2[l - 1]l - 1]]) ? dp[i + p2[l - 1]l - 1] : dp[il - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr[dp[ldx]] > depthArr[dp[r - p2[dx]dx]]) return dp[r - p2[dx]dx]; else return dp[ldx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.Add(cur); // Incrementing euler walk pointer ptr++; foreach (int x in adj[cur]) { if (x != prev) { dfs(x cur dep + 1); euler.Add(cur); ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { foreach (int x in euler) depthArr.Add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } static void addEdge(int u int v) { adj[u].Add(v); adj[v].Add(u); } // Driver Code static void Main(string[] args) { int sz = 9; adj = new List<int>[sz]; for (int i = 0; i < sz; i++) { adj[i] = new List<int>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Array.Fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.Count); Console.WriteLine('LCA(67) : ' + LCA(6 7)); Console.WriteLine('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by Prince Kumar
let adj = []; for (let _ = 0; _ < 101; _++) { adj.push([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array(101).fill(-1); // stores depth for all nodes in the tree let level = new Array(101).fill(0); // pointer to euler walk let ptr = 0; // sparse table let dp = []; for (let _ = 0; _ < 101; _++) { dp.push(new Array(18).fill(-1)); } // stores log values let logn = new Array(101).fill(0); // stores power of 2 let p2 = new Array(20).fill(0); function buildSparseTable(n) { // initializing sparse table for (let i = 0; i < n; i++) { dp[i][0] = i - 1 >= 0 && depthArr[i] > depthArr[i - 1] ? i - 1 : i; } // dp to fill sparse table for (let l = 1; l < 15; l++) { for (let i = 0; i < n; i++) { if ( dp[i][l - 1] !== -1 && dp[i + p2[l - 1]][l - 1] !== -1 ) { dp[i][l] = depthArr[dp[i][l - 1]] > depthArr[dp[i + p2[l - 1]][l - 1]] ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; } else { break; } } } } function query(l r) { let d = r - l; let dx = logn[d]; if (l === r) { return l; } if (depthArr[dp[l][dx]] > depthArr[dp[r - p2[dx]][dx]]) { return dp[r - p2[dx]][dx]; } else { return dp[l][dx]; } } function preprocess() { // memorizing powers of 2 p2[0] = 1; for (let i = 1; i < 18; i++) { p2[i] = p2[i - 1] * 2; } // memorizing all log(n) values let val = 1; ptr = 0; for (let i = 1; i < 101; i++) { logn[i] = ptr - 1; if (val === i) { val *= 2; logn[i] = ptr; ptr += 1; } } } function dfs(cur prev dep) { // marking FAI for cur node if (FAI[cur] === -1) { FAI[cur] = ptr; } level[cur] = dep; // pushing root to euler walk euler.push(cur); // incrementing euler walk pointer ptr += 1; for (let x of adj[cur]) { if (x !== prev) { dfs(x cur dep + 1); // pushing cur again in backtrack // of euler walk euler.push(cur); // increment euler walk pointer ptr += 1; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr() { for (let x of euler) { depthArr.push(level[x]); } } function LCA(u v) { // trivial case if (u === v) { return u; } if (FAI[u] > FAI[v]) { [u v] = [v u]; } // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } function addEdge(u v) { adj[u].push(v); adj[v].push(u); } // constructing the described tree let numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; FAI = new Array(numberOfNodes + 1).fill(-1); dfs(1 0 0); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.length); console.log('LCA(67) : ' LCA(6 7)); console.log('LCA(64) : ' LCA(6 4));
الإخراج
LCA(67) : 1 LCA(64) : 2
ملحوظة : نحن نجري حسابًا مسبقًا لجميع الطاقة المطلوبة للرقم 2 ونقوم أيضًا بحساب جميع قيم السجل المطلوبة مسبقًا لضمان التعقيد الزمني الثابت لكل استعلام. وإلا، إذا قمنا بتسجيل الحساب لكل عملية استعلام، فلن يكون تعقيد الوقت لدينا ثابتًا.
تعقيد الوقت: تتم عملية التحويل من LCA إلى RMQ بواسطة Euler Walk الذي يستغرق على) وقت.
تستغرق المعالجة المسبقة للجدول المتناثر في RMQ وقتًا (تسجيل الدخول) والإجابة على كل استعلام هي عملية زمنية ثابتة. لذلك فإن التعقيد الزمني الإجمالي هو O(nlogn) - المعالجة المسبقة و يا(1) لكل استعلام.
المساحة المساعدة: يا(ن+ق)
إضافة سلسلة
إنشاء اختبار
