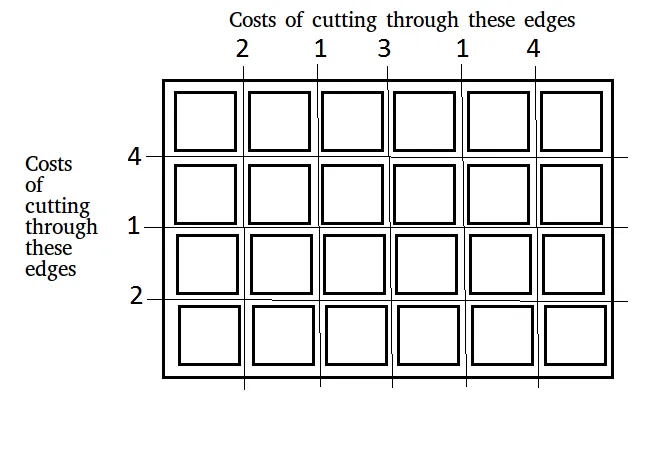
نظرا لمجلس الأبعاد ن × م التي يجب تقطيعها إلى مربعات n × m. يتم توفير تكلفة القطع على طول الحافة الأفقية أو الرأسية في صفيفين:

• س[] : خفض التكاليف على طول الحواف الرأسية (بالطول).
• و[] : خفض التكاليف على طول الحواف الأفقية (من حيث العرض).

أوجد أقل تكلفة إجمالية مطلوبة لتقطيع اللوحة إلى مربعات على النحو الأمثل.

أمثلة: 

مدخل: س[] = [2 1 3 1 4] ص [] = [4 1 2] ن = 4 م = 6
الإخراج: 42
توضيح:

في البداية لا. من القطاعات الأفقية = 1 و لا. القطاعات العمودية = 1
الطريقة المثلى للتقطيع إلى مربعات هي:
اختر 4 (من x) -> تكلفة القطع الرأسي = 4 × المقاطع الأفقية = 4
 الآن المقاطع الأفقية = 1 المقاطع الرأسية = 2.
اختر 4 (من y) -> تكلفة القطع الأفقي = 4 × القطاعات الرأسية = 8
 الآن المقاطع الأفقية = 2 شرائح رأسية = 2.
اختر 3 (من x) -> تكلفة القطع العمودي = 3 × المقاطع الأفقية = 6
 الآن المقاطع الأفقية = 2 شرائح رأسية = 3.
اختر 2 (من x) -> تكلفة القطع الرأسي = 2 × المقاطع الأفقية = 4
 الآن المقاطع الأفقية = 2 شرائح رأسية = 4.
اختر 2 (من y) -> تكلفة القطع الأفقي = 2 × المقاطع الرأسية = 8
 الآن المقاطع الأفقية = 3 شرائح رأسية = 4.
اختر 1 (من x) -> تكلفة القطع الرأسي = 1 × المقاطع الأفقية = 3
الآن المقاطع الأفقية = 3 شرائح رأسية = 5.
اختر 1 (من x) -> تكلفة القطع الرأسي = 1 × المقاطع الأفقية = 3
الآن المقاطع الأفقية = 3 شرائح رأسية = 6.
اختر 1 (من y) -> تكلفة القطع الأفقي = 1 × المقاطع الرأسية = 6
الآن المقاطع الأفقية = 4 شرائح رأسية = 6.
إذن التكلفة الإجمالية = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

مدخل: x[] = [1 1 1] y[] = [1 1 1] n = 4 م = 4
الإخراج: 15
توضيح:
في البداية لا. من القطاعات الأفقية = 1 و لا. القطاعات العمودية = 1
الطريقة المثلى للتقطيع إلى مربعات هي:
اختر 1 (من y) -> تكلفة القطع الأفقي = 1 × المقاطع الرأسية = 1
الآن المقاطع الأفقية = 2 شرائح رأسية = 1.
اختر 1 (من y) -> تكلفة القطع الأفقي = 1 × المقاطع الرأسية = 1
الآن المقاطع الأفقية = 3 شرائح رأسية = 1.
اختر 1 (من y) -> تكلفة القطع الأفقي = 1 × المقاطع الرأسية = 1
الآن المقاطع الأفقية = 4 شرائح رأسية = 1.
اختر 1 (من x) -> تكلفة القطع العمودي = 1 × المقاطع الأفقية = 4
الآن المقاطع الأفقية = 4 شرائح رأسية = 2.
اختر 1 (من x) -> تكلفة القطع العمودي = 1 × المقاطع الأفقية = 4
الآن المقاطع الأفقية = 4 شرائح رأسية = 3.
اختر 1 (من x) -> تكلفة القطع العمودي = 1 × المقاطع الأفقية = 4
الآن المقاطع الأفقية = 4 شرائح رأسية = 4
إذن التكلفة الإجمالية = 1 + 1 + 1 + 4 + 4 + 4 = 15.

جدول المحتويات

• [نهج ساذج] جرب جميع التباديل - O((n+m)!×(n+m)) الوقت وO(n+m) الفضاء
• [النهج المتوقع] استخدام تقنية الجشع - O( n (log n)+m (log m)) الوقت وO(1) الفضاء

[نهج ساذج] جرب جميع التباديل - O((n+m)!×(n+m)) الوقت وO(n+m) الفضاء

تتمثل الفكرة في إنشاء جميع التباديل الممكنة للتخفيضات المحددة ثم حساب تكلفة كل تبديل. وأخيرا إرجاع الحد الأدنى من التكلفة فيما بينهم.

ملحوظة: هذا النهج غير ممكن بالنسبة للمدخلات الأكبر لأن عدد التباديل ينمو بشكل مضروب مثل (m+n-2) !.
لكل التقليب يجب علينا حساب التكلفة في الوقت O(m+n). ومن ثم يصبح التعقيد الزمني الإجمالي O((m+n−2)!×(m+n)).

[النهج المتوقع] استخدام تقنية الجشع - O( n (log n)+m (log m)) الوقت وO(1) الفضاء

تكمن الفكرة في إجراء التخفيضات الأكثر تكلفة أولاً باستخدام ملف النهج الجشع . الملاحظة هي أن اختيار أعلى خفض للتكلفة في كل خطوة يقلل من التكاليف المستقبلية من خلال التأثير على أجزاء متعددة في وقت واحد. نقوم بفرز تكاليف الخفض الرأسي (x) والأفقي (y) بترتيب تنازلي ثم نختار التكلفة الأكبر بشكل متكرر لتحقيق أقصى قدر من التوفير في التكاليف. تتم معالجة القطع المتبقية بشكل منفصل لضمان تقسيم جميع الأقسام على النحو الأمثل.

ماذا يحدث عندما نقوم بإجراء قطع؟

• قطع أفقي → أنت تقطع العرض وبالتالي يزيد عدد الشرائط الأفقية (hCount++). ولكن يتم ضرب التكلفة في vCount (عدد الشرائط الرأسية) لأن القطع الأفقي يجب أن يمر عبر جميع المقاطع الرأسية.
• قطع عمودي → أنت تقطع الارتفاع وبالتالي يزيد عدد الشرائط الرأسية (vCount++). ولكن يتم ضرب التكلفة في hCount (عدد الشرائط الأفقية) لأن القطع الرأسي يجب أن يمر عبر جميع المقاطع الأفقية.

خطوات حل المشكلة:

• قم بفرز المصفوفتين x وy بترتيب تنازلي.
• استخدم مؤشرين، أحدهما لـ x والآخر لـ y بدءًا من القيمة الأكبر والانتقال نحو القيم الأصغر.
• احتفظ بـ hCount وvCount لتتبع عدد المقاطع التي يؤثر عليها كل قطع وتحديثها وفقًا لذلك.
• كرر بينما يحتوي كل من x وy على عمليات قطع غير معالجة، مع اختيار التكلفة الأكبر دائمًا لتقليل النفقات الإجمالية.
• إذا كان x يحتوي على قطع متبقية، فقم بمعالجتها باستخدام مضاعف hCount؛ وبالمثل، يمكنك معالجة عمليات القطع المتبقية باستخدام vCount.
• قم بتجميع التكلفة الإجمالية في كل خطوة باستخدام الصيغة: خفض التكلفة * عدد القطع المتأثرة مما يضمن الحد الأدنى من التكلفة.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42