Random Forest هي خوارزمية شائعة للتعلم الآلي تنتمي إلى تقنية التعلم الخاضع للإشراف. ويمكن استخدامه لكل من مشاكل التصنيف والانحدار في ML. وهو يقوم على مفهوم التعلم الجماعي, وهي عملية الجمع بين عدة مصنفات لحل مشكلة معقدة وتحسين أداء النموذج.
حسب الاسم المقترح، 'الغابات العشوائية عبارة عن مصنف يحتوي على عدد من أشجار القرار في مجموعات فرعية مختلفة من مجموعة البيانات المحددة ويأخذ المتوسط لتحسين الدقة التنبؤية لمجموعة البيانات تلك.' بدلاً من الاعتماد على شجرة قرار واحدة، تأخذ الغابة العشوائية التنبؤ من كل شجرة وعلى أساس أغلبية أصوات التنبؤات، وتتنبأ بالمخرج النهائي.
يؤدي العدد الأكبر من الأشجار في الغابة إلى دقة أعلى ويمنع مشكلة التجهيز الزائد.
حاول التقاط Java
يشرح الرسم البياني أدناه عمل خوارزمية Random Forest:
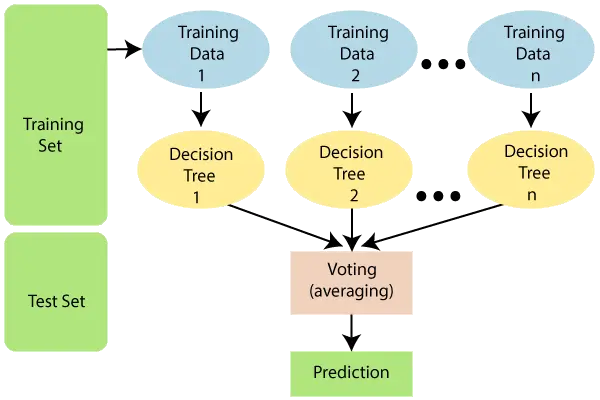
ملحوظة: لفهم خوارزمية الغابة العشوائية بشكل أفضل، يجب أن تكون لديك معرفة بخوارزمية شجرة القرار.
افتراضات للغابات العشوائية
نظرًا لأن الغابة العشوائية تجمع بين أشجار متعددة للتنبؤ بفئة مجموعة البيانات، فمن الممكن أن تتنبأ بعض أشجار القرار بالإخراج الصحيح، بينما قد لا تتنبأ أشجار أخرى. لكن معًا، تتنبأ جميع الأشجار بالنتيجة الصحيحة. ولذلك، فيما يلي افتراضان لمصنف مجموعة عشوائية أفضل:
- يجب أن تكون هناك بعض القيم الفعلية في متغير الميزة لمجموعة البيانات حتى يتمكن المصنف من التنبؤ بنتائج دقيقة بدلاً من النتيجة المخمنة.
- يجب أن يكون للتنبؤات من كل شجرة ارتباطات منخفضة جدًا.
لماذا استخدام الغابة العشوائية؟
فيما يلي بعض النقاط التي تشرح لماذا يجب علينا استخدام خوارزمية Random Forest:
- يستغرق وقتًا أقل في التدريب مقارنة بالخوارزميات الأخرى.
- فهو يتنبأ بالمخرجات بدقة عالية، حتى بالنسبة لمجموعة البيانات الكبيرة التي يعمل بها بكفاءة.
- ويمكنه أيضًا الحفاظ على الدقة عند فقدان نسبة كبيرة من البيانات.
كيف تعمل خوارزمية الغابة العشوائية؟
تعمل الغابة العشوائية على مرحلتين، الأولى هي إنشاء الغابة العشوائية من خلال الجمع بين شجرة القرار N، والثانية هي عمل تنبؤات لكل شجرة تم إنشاؤها في المرحلة الأولى.
يمكن شرح عملية العمل في الخطوات والرسم البياني أدناه:
تسلسل إلى الأمام
الخطوة 1: حدد نقاط بيانات K عشوائية من مجموعة التدريب.
الخطوة 2: قم ببناء أشجار القرار المرتبطة بنقاط البيانات المحددة (المجموعات الفرعية).
الخطوه 3: اختر الرقم N لأشجار القرار التي تريد بنائها.
الخطوة 4: كرر الخطوة 1 و2.
الخطوة 5: بالنسبة لنقاط البيانات الجديدة، ابحث عن تنبؤات كل شجرة قرارات، وقم بتعيين نقاط البيانات الجديدة للفئة التي تفوز بأغلبية الأصوات.
يمكن فهم عمل الخوارزمية بشكل أفضل من خلال المثال التالي:
مثال: لنفترض أن هناك مجموعة بيانات تحتوي على صور فواكه متعددة. لذلك، يتم إعطاء مجموعة البيانات هذه إلى مصنف الغابة العشوائي. يتم تقسيم مجموعة البيانات إلى مجموعات فرعية وتعطى لكل شجرة قرار. خلال مرحلة التدريب، تنتج كل شجرة قرار نتيجة تنبؤ، وعندما تحدث نقطة بيانات جديدة، بناءً على غالبية النتائج، يتنبأ مصنف Random Forest بالقرار النهائي. النظر في الصورة أدناه:

تطبيقات الغابة العشوائية
هناك أربعة قطاعات تستخدم فيها الغابات العشوائية في الغالب:
مزايا الغابة العشوائية
- Random Forest قادرة على أداء مهام التصنيف والانحدار.
- إنه قادر على التعامل مع مجموعات البيانات الكبيرة ذات الأبعاد العالية.
- إنه يعزز دقة النموذج ويمنع مشكلة التجهيز الزائد.
مساوئ الغابة العشوائية
- على الرغم من أنه يمكن استخدام الغابة العشوائية لكل من مهام التصنيف والانحدار، إلا أنها ليست أكثر ملاءمة لمهام الانحدار.
تنفيذ بايثون لخوارزمية الغابة العشوائية
سنقوم الآن بتنفيذ شجرة خوارزمية الغابة العشوائية باستخدام لغة بايثون. ولهذا، سوف نستخدم نفس مجموعة البيانات 'user_data.csv'، التي استخدمناها في نماذج التصنيف السابقة. باستخدام نفس مجموعة البيانات، يمكننا مقارنة مصنف Random Forest بنماذج التصنيف الأخرى مثل مصنف شجرة القرار, كي إن إن، SVM، الانحدار اللوجستي، الخ.
خطوات التنفيذ موضحة أدناه:
طريقة سلسلة فرعية جافا
- خطوة المعالجة المسبقة للبيانات
- ملاءمة خوارزمية الغابة العشوائية لمجموعة التدريب
- التنبؤ بنتيجة الاختبار
- دقة اختبار النتيجة (إنشاء مصفوفة الارتباك)
- تصور نتيجة مجموعة الاختبار.
1. خطوة المعالجة المسبقة للبيانات:
فيما يلي رمز خطوة المعالجة المسبقة:
# importing libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd #importing datasets data_set= pd.read_csv('user_data.csv') #Extracting Independent and dependent Variable x= data_set.iloc[:, [2,3]].values y= data_set.iloc[:, 4].values # Splitting the dataset into training and test set. from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.25, random_state=0) #feature Scaling from sklearn.preprocessing import StandardScaler st_x= StandardScaler() x_train= st_x.fit_transform(x_train) x_test= st_x.transform(x_test)
في الكود أعلاه، قمنا بمعالجة البيانات مسبقًا. حيث قمنا بتحميل مجموعة البيانات، والتي تعطى على النحو التالي:

2. ملاءمة خوارزمية الغابة العشوائية لمجموعة التدريب:
الآن سوف نلائم خوارزمية الغابة العشوائية مع مجموعة التدريب. لتناسب ذلك، سوف نقوم باستيراد RandomForestClassifier فئة من sklearn.ensemble مكتبة. وفيما يلي التعليمات البرمجية:
#Fitting Decision Tree classifier to the training set from sklearn.ensemble import RandomForestClassifier classifier= RandomForestClassifier(n_estimators= 10, criterion='entropy') classifier.fit(x_train, y_train)
في الكود أعلاه، يأخذ كائن المصنف المعلمات التالية:
انتاج:
الإدراج بيثون
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='entropy', max_depth=None, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None, oob_score=False, random_state=None, verbose=0, warm_start=False)
3. توقع نتيجة مجموعة الاختبار
وبما أن نموذجنا ملائم لمجموعة التدريب، فيمكننا الآن التنبؤ بنتيجة الاختبار. للتنبؤ، سنقوم بإنشاء متجه تنبؤ جديد y_pred. أدناه هو رمز لذلك:
#Predicting the test set result y_pred= classifier.predict(x_test)
انتاج:
يتم إعطاء متجه التنبؤ على النحو التالي:

من خلال التحقق من متجه التنبؤ أعلاه واختبار مجموعة المتجهات الحقيقية، يمكننا تحديد التنبؤات غير الصحيحة التي أجراها المصنف.
4. إنشاء مصفوفة الارتباك
الآن سوف نقوم بإنشاء مصفوفة الارتباك لتحديد التوقعات الصحيحة وغير الصحيحة. أدناه هو رمز لذلك:
#Creating the Confusion matrix from sklearn.metrics import confusion_matrix cm= confusion_matrix(y_test, y_pred)
انتاج:

كما نرى في المصفوفة أعلاه، هناك 4+4= 8 توقعات غير صحيحة و 64+28= 92 توقعاً صحيحاً.
5. تصور نتيجة مجموعة التدريب
هنا سوف نتصور نتيجة مجموعة التدريب. لتصور نتيجة مجموعة التدريب، سنقوم برسم رسم بياني لمصنف الغابة العشوائية. سوف يتنبأ المصنف بنعم أو لا للمستخدمين الذين اشتروا أو لم يشترو سيارة الدفع الرباعي كما فعلنا في الانحدار اللوجستي. أدناه هو رمز لذلك:
from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
انتاج:
xor في جافا

الصورة أعلاه هي نتيجة التصور لمصنف Random Forest الذي يعمل مع نتيجة مجموعة التدريب. إنه مشابه جدًا لمصنف شجرة القرار. تتوافق كل نقطة بيانات مع كل مستخدم لبيانات المستخدم، والمناطق الأرجوانية والخضراء هي مناطق التنبؤ. المنطقة الأرجوانية مخصصة للمستخدمين الذين لم يشتروا السيارة ذات الدفع الرباعي، والمنطقة الخضراء مخصصة للمستخدمين الذين اشتروا السيارة ذات الدفع الرباعي.
لذلك، في مصنف الغابة العشوائية، أخذنا 10 أشجار تنبأت بنعم أو لا للمتغير الذي تم شراؤه. أخذ المصنف غالبية التوقعات وقدم النتيجة.
6. تصور نتيجة مجموعة الاختبار
الآن سوف نقوم بتصور نتيجة مجموعة الاختبار. أدناه هو رمز لذلك:
#Visulaizing the test set result from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm(Test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
انتاج:

الصورة أعلاه هي نتيجة التصور لمجموعة الاختبار. يمكننا التحقق من وجود حد أدنى لعدد التنبؤات غير الصحيحة (8) دون مشكلة التجهيز الزائد. سنحصل على نتائج مختلفة عن طريق تغيير عدد الأشجار في المصنف.
