• يُعرف أيضًا مشغل Bitwise XOR باسم حصري أو
• يتم الإشارة إليه باستخدام '^'
• كما هو واضح من الاسم، فهو يعمل على مستوى قليلا من المعاملات.
• لقد أصبح مشغل Bitwise XOR ضمن فئة مشغلي Bitwise.
• في عامل التشغيل OR الحصري للبت (XOR)، يلزم وجود معاملين، ويتم فصل هذين المعاملين برمز XOR، أي '^'.
• لتحديد المخرج أو النتيجة التي تخرج بعد تطبيق عامل XOR على معاملين، نحتاج إلى اتباع جدول الحقيقة المنطقية لعامل XOR.
• XOR Truth Table هو جدول رياضي تم إنشاؤه باستخدام المنطق الصحيح لمشغل XOR.
• المنطق المستخدم وراء عامل XOR هو؛ كلما تم تطبيق عملية XOR على الاثنين مختلف بتات من معاملين، فإن النتيجة ستنتج دائمًا '1'، وإذا تم تطبيق عملية XOR على الاثنين نفس بتات من معاملين فإن النتيجة تنتج مخرجات '0'.

جدول الحقيقة لمشغل OR (XOR) الحصري

يجب أن يكون هناك معاملان؛ الأول هو A والثاني هو B، وسيكون إجمالي مجموعات المدخلات المتكونة من هذين المعاملين 4. وباستخدام جدول الحقيقة XOR التالي، سنحدد المخرجات المقابلة. سيتم التقاط النتيجة في C، هنا ج = أ ^ ب.

في جدول الحقيقة هذا، نأخذ المدخلات على شكل بتات، أي 0 و1، وسيتم إنشاء المخرجات أيضًا على شكل بتات، أي 0 و1.

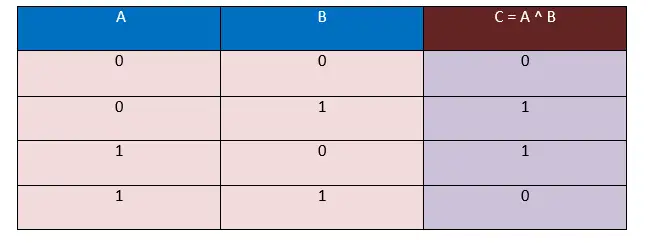
هنا، في جدول الحقيقة XOR أعلاه، نلاحظ أنه عندما تكون قيم المعاملات A و B مختلفة، أي (0, 1)، (1, 0)، فإن النتيجة التي تظهر ستكون دائمًا 1. وعندما تكون قيم المعاملين A وB هي نفسها، أي (0, 0)، (1, 1)، والنتيجة التي تظهر ستكون دائمًا 0.

وبالمثل، بهذه الطريقة، يمكننا رسم جدول الصواب لـ منطقية قيم -

يجب أن يكون هناك معاملان؛ اول واحد هو أ والثاني هو ب . سيكون مجموع مجموعات المدخلات التي شكلها هذين المعاملين هو 4. وباستخدام جدول الحقيقة XOR التالي، سنحدد المخرجات المقابلة. سيتم التقاط النتيجة في C، هنا C = A ^ B.

في جدول الحقيقة هذا، نأخذ المدخلات في شكل قيم الحقيقة، أي True ( T ) و False ( F ). سيتم أيضًا إنشاء المخرجات في شكل قيم حقيقية، أي T وF.

هنا، في جدول الحقيقة XOR أعلاه، نلاحظ أنه عندما تكون قيم المعاملات A و B مختلفة، أي (F, T)، (T, F)، فإن النتيجة ستكون دائمًا T. وعندما يكون قيم المعاملين A وB متماثلتان، أي (F, F)، (T, T)، وستكون النتيجة دائمًا F.

ومن الجداول أعلاه نلاحظ ذلك يُشار إلى T (صحيح) بالرقم واحد ويُشار إلى F (خطأ) بالرمز 0.

خطوات حل أي مشكلة -

1. ستكون المعاملات الواردة في المشكلة دائمًا بالقيمة العشرية.
2. أولا، نحن بحاجة إلى تحويل قيم المعاملات إلى الثنائية
3. بعد تحويل قيم المعاملات إلى أرقام ثنائية، ضع كلا المعاملين واحدًا فوق بعضهما البعض.
4. تذكر أنه قبل تطبيق عملية OR (XOR) الحصرية عليها، يرجى التحقق من عدد الأرقام فيهم.
5. إذا لم يتطابق عدد الأرقام، فإن الصفر الإضافي الموجود في الطرف الأيسر من المعامل الصغير يوازن عدد الأرقام.
6. أخيرًا، بمساعدة جدول الحقيقة أعلاه، قم بتطبيق عملية XOR على المعاملات واحدًا تلو الآخر، مع أخذ بت واحد في كل مرة لتطبيق عملية XOR.
7. وأخيرا، يتم إنتاج النتيجة في شكل مخرجات.
8. سيكون الناتج الناتج في شكل ثنائي، والآن قم بتحويل النموذج الثنائي إلى شكل عشري وقم بتدوين القيمة الناتجة.

تنفيذ عملية Bitwise Exclusive OR (XOR) في لغة C++

دعونا نفهم بمزيد من التفاصيل حول تنفيذ عملية XOR في لغة C++ بمساعدة الأمثلة -

مثال 1: ابحث عن OR الحصري لقيم الأعداد الصحيحة؛ 10 و 14. واشرحها أيضًا واكتب كود التنفيذ بلغة C++.

حل: دعونا نفكر في متغيرين، 'a' و'b'، لتخزين المعاملين المقابلين الواردين في السؤال أعلاه، أي 10 و14.

هنا أ = 10 و ب = 14.

سوف نتبع الخطوات التالية لمعرفة OR الحصري للمعاملين المحددين.

1. نحن نعلم أن 10 و 14 في شكل عشري، ولتطبيق عملية XOR ذات البتات، من الضروري تحويلها إلى شكل ثنائي.
2. الشكل الثنائي 'a'، أي 10 هو '1010' والشكل الثنائي لـ 'b'، أي 14 هو '1110'.
3. نلاحظ هنا أن عدد الأرقام الثنائية الموجودة في a هو أربعة وعدد الأرقام الثنائية الموجودة في b هو أيضًا 4؛ ومن ثم فإن عدد الأرقام الثنائية الموجودة في كلا المتغيرين هو نفسه ومتوازن بالفعل، ولا نحتاج إلى إضافة عدد أكبر من الأصفار لتحقيق التوازن.
4. الآن، قم بتوزيع الأرقام الثنائية الموجودة في 'b' على الأرقام الثنائية الموجودة في 'a'.
5. وأخيرًا، فإن تطبيق عملية XOR واحدًا تلو الآخر على البتات المقابلة يطابق ويسجل المخرجات.
6. سيكون الناتج الذي تم إنشاؤه أخيرًا في شكل ثنائي، كما هو موضح في السؤال أعلاه في النموذج العشري، لذلك نحتاج إلى تحويل النتيجة إلى شكل عشري.

توضيح:

أ = 10 (بالصيغة العشرية)

أونكليك شبيبة

ب = 14 (بالصيغة العشرية)

الآن، بالنسبة إلى XOR b، نحتاج إلى تحويل a وb في شكل ثنائي -

أ = 1010 (في شكل ثنائي)

ب = 1110 (في شكل ثنائي)

الآن، تطبيق عملية XOR على a وb -

أ = 1010

ب = 1110

---------------

أ ^ ب = 0100 (في شكل ثنائي)

نتيجة a ^ b هي 0100، وهي في شكل ثنائي.

الآن قم بتحويل النتيجة إلى شكل عشري، وهو 4.

10^14 = 4

ملاحظة: باستخدام جدول الحقيقة XOR أعلاه، يتم إنشاء إخراج البتات المقابلة.

سنقوم الآن بتطبيق عملية bitwise XOR على 10 و14 بلغة C++ وسنحصل على النتيجة، أي 4.

رمز C++ للمثال أعلاه:

 //************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout &lt;&gt; b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout &lt;&lt; &apos;Applying XOR operation on a and b: &apos;&lt;&lt; endl ; cout &lt;&lt; &apos;a ^ b = &apos; &lt;&lt; c &lt;&lt; endl ; // Printing the output } </'>

انتاج |

الاتصالات المحجوبة

مثال 2: ابحث عن OR الحصري لقيم الأعداد الصحيحة؛ 3 و 15. واشرحها أيضًا واكتب كود التنفيذ بلغة C++.

حل: دعونا نفكر في متغيرين، 'a' و'b'، لتخزين المعاملين المقابلين الواردين في السؤال أعلاه، أي 3 و15.

هنا أ = 3 و ب = 15.

سوف نتبع الخطوات التالية لمعرفة OR الحصري للمعاملين المحددين.

1. نحن نعلم أن 3 و 15 في شكل عشري، ولتطبيق عملية XOR ذات البتات، من الضروري تحويلها إلى شكل ثنائي.
2. الشكل الثنائي 'a'، أي 3 هو 'أحد عشر' والشكل الثنائي لـ 'b'، أي 15 هو '1111'.
3. سنلاحظ هنا أن عدد الأرقام الثنائية الموجودة في a هو اثنان وعدد الأرقام الثنائية الموجودة في b هو أربعة؛ وبالتالي فإن عدد الأرقام الثنائية الموجودة في كلا المتغيرين ليس هو نفسه. وبالتالي، في حالة عدم التوازن، نحتاج إلى إضافة عدد أكبر من الأصفار على الجانب الأيسر من الرقم الثنائي السفلي، أي a، وهو ' أحد عشر' ، لتحقيق التوازن فيه.
4. بعد الموازنة، قيمة a هي '0011' ، و ب هو '1111'.
5. الآن، قم بتوزيع الأرقام الثنائية الموجودة في 'b' على الأرقام الثنائية الموجودة في 'a'.
6. وأخيرًا، فإن تطبيق عملية XOR واحدًا تلو الآخر على البتات المقابلة يطابق ويسجل المخرجات.
7. سيكون الناتج الذي تم إنشاؤه أخيرًا في شكل ثنائي، كما هو موضح في السؤال أعلاه في النموذج العشري، لذلك نحتاج إلى تحويل النتيجة إلى شكل عشري.

توضيح:

أ = 3 (بالصيغة العشرية)

ب = 15 (بالصيغة العشرية)

الآن، بالنسبة إلى XOR b، نحتاج إلى تحويل a وb في شكل ثنائي -

أ = 0011 (في شكل ثنائي)

ب = 1111 (في شكل ثنائي)

الآن، تطبيق عملية XOR على a وb -

أ = 0011

ب = 1111

---------------

أ ^ ب = 1100 (في شكل ثنائي)

نتيجة a ^ b هي 1100، وهي في شكل ثنائي.

الآن قم بتحويل النتيجة إلى شكل عشري، وهو 12.

3^15 = 12

ملاحظة: باستخدام جدول الحقيقة XOR أعلاه، يتم إنشاء إخراج البتات المقابلة.

سنقوم الآن بتطبيق عملية bitwise XOR على 3 و15 بلغة C++ وسنحصل على النتيجة، أي 12.

رمز C++ للمثال أعلاه:

 //************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout &lt;&gt; b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout &lt;&lt; &apos;Applying XOR operation on a and b: &apos;&lt;&lt; endl ; cout &lt;&lt; &apos;a ^ b = &apos; &lt;&lt; c &lt;&lt; endl ; // Printing the output } </'>

انتاج |