البرمجة الديناميكية هي تقنية تقوم بتقسيم المشاكل إلى مسائل فرعية، وحفظ النتيجة لأغراض مستقبلية حتى لا نحتاج لحساب النتيجة مرة أخرى. يتم تحسين المشاكل الفرعية لتحسين الحل الشامل المعروف باسم خاصية البنية التحتية المثالية. الاستخدام الرئيسي للبرمجة الديناميكية هو حل مشاكل التحسين. هنا، تعني مشاكل التحسين أنه عندما نحاول معرفة الحد الأدنى أو الحد الأقصى لحل المشكلة. تضمن البرمجة الديناميكية إيجاد الحل الأمثل للمشكلة في حالة وجود الحل.
يقول تعريف البرمجة الديناميكية إنها تقنية لحل مشكلة معقدة عن طريق تقسيم مجموعة من المشكلات الفرعية الأبسط أولاً، وحل كل مشكلة فرعية مرة واحدة فقط، ثم تخزين حلولها لتجنب الحسابات المتكررة.
دعونا نفهم هذا النهج من خلال مثال.
النظر في مثال على سلسلة فيبوناتشي. السلسلة التالية هي سلسلة فيبوناتشي:
تعيين محدد جافا
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,,…
لم يتم حساب الأرقام في السلسلة أعلاه بشكل عشوائي. رياضياً، يمكننا كتابة كل مصطلح باستخدام الصيغة التالية:
و(ن) = و(ن-1) + و(ن-2)،
مع القيم الأساسية F(0) = 0، وF(1) = 1. لحساب الأرقام الأخرى، نتبع العلاقة المذكورة أعلاه. على سبيل المثال، F(2) هو المجموع و(0) و و (1)، وهو ما يعادل 1.
كيف يمكننا حساب F(20)؟
سيتم حساب الحد F(20) باستخدام الصيغة n لسلسلة فيبوناتشي. يوضح الشكل أدناه كيفية حساب F(20).
الباندا الانحراف المعياري
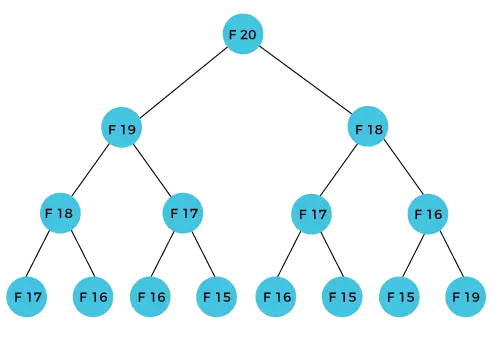
كما يمكننا أن نلاحظ في الشكل أعلاه أن F(20) يتم حسابه كمجموع F(19) وF(18). في منهج البرمجة الديناميكية نحاول تقسيم المشكلة إلى مشكلات فرعية متشابهة. نحن نتبع هذا النهج في الحالة المذكورة أعلاه حيث يتم حل F(20) في المسائل الفرعية المشابهة، أي F(19) وF(18). إذا قمنا بتلخيص تعريف البرمجة الديناميكية الذي ينص على أنه لا ينبغي حساب المشكلة الفرعية المشابهة أكثر من مرة. ومع ذلك، في الحالة المذكورة أعلاه، يتم حساب المشكلة الفرعية مرتين. في المثال أعلاه، يتم حساب F(18) مرتين؛ وبالمثل، يتم حساب F(17) أيضًا مرتين. ومع ذلك، فإن هذه التقنية مفيدة جدًا لأنها تحل المشكلات الفرعية المشابهة، ولكن يجب أن نكون حذرين أثناء تخزين النتائج لأننا لا نهتم بتخزين النتيجة التي قمنا بحسابها مرة واحدة، ومن ثم يمكن أن يؤدي ذلك إلى إهدار الموارد.
في المثال أعلاه، إذا قمنا بحساب F(18) في الشجرة الفرعية اليمنى، فإن ذلك يؤدي إلى استخدام هائل للموارد ويقلل الأداء العام.
الحل للمشكلة المذكورة أعلاه هو حفظ النتائج المحسوبة في مصفوفة. أولاً، نحسب F(16) وF(17) ونحفظ قيمهما في مصفوفة. يتم حساب F(18) عن طريق جمع قيم F(17) وF(16)، المحفوظة بالفعل في صفيف. يتم حفظ القيمة المحسوبة لـ F(18) في مصفوفة. يتم حساب قيمة F(19) باستخدام مجموع F(18) وF(17)، ويتم حفظ قيمها بالفعل في مصفوفة. يتم تخزين القيمة المحسوبة لـ F(19) في صفيف. يمكن حساب قيمة F(20) عن طريق إضافة قيم F(19) وF(18)، ويتم تخزين قيم كل من F(19) وF(18) في مصفوفة. يتم تخزين القيمة المحسوبة النهائية لـ F(20) في مصفوفة.
كيف يعمل نهج البرمجة الديناميكية؟
فيما يلي الخطوات التي تتبعها البرمجة الديناميكية:
- فهو يقسم المشكلة المعقدة إلى مشاكل فرعية أبسط.
- ويجد الحل الأمثل لهذه المشاكل الفرعية.
- يقوم بتخزين نتائج المسائل الفرعية (الحفظ). تُعرف عملية تخزين نتائج المشكلات الفرعية بالحفظ.
- ويعيد استخدامها بحيث يتم حساب نفس المشكلة الفرعية أكثر من مرة.
- وأخيرًا، احسب نتيجة المشكلة المعقدة.
الخطوات الخمس المذكورة أعلاه هي الخطوات الأساسية للبرمجة الديناميكية. البرمجة الديناميكية قابلة للتطبيق والتي لها خصائص مثل:
تعدد الأشكال
تلك المشاكل التي تحتوي على مشاكل فرعية متداخلة وبنيات أساسية مثالية. هنا، البنية التحتية المثالية تعني أنه يمكن الحصول على حل مشاكل التحسين ببساطة عن طريق الجمع بين الحل الأمثل لجميع المشاكل الفرعية.
في حالة البرمجة الديناميكية، سيزداد التعقيد المكاني عندما نقوم بتخزين النتائج الوسيطة، لكن التعقيد الزمني سينخفض.
أساليب البرمجة الديناميكية
هناك طريقتان للبرمجة الديناميكية:
- النهج من أعلى إلى أسفل
- نهج من أسفل إلى أعلى
النهج من أعلى إلى أسفل
يتبع المنهج التنازلي أسلوب الحفظ، بينما يتبع المنهج التنازلي أسلوب الجدولة. الحفظ هنا يساوي مجموع العودية والتخزين المؤقت. التكرار يعني استدعاء الوظيفة نفسها، في حين أن التخزين المؤقت يعني تخزين النتائج المتوسطة.
الهياكل باستخدام المصفوفات في ج
مزايا
- فمن السهل جدا أن نفهم وتنفيذها.
- فهو يحل المشاكل الفرعية فقط عندما يكون ذلك مطلوبا.
- من السهل تصحيح الأخطاء.
سلبيات
ويستخدم تقنية العودية التي تشغل المزيد من الذاكرة في مكدس الاستدعاءات. في بعض الأحيان عندما يكون التكرار عميقًا جدًا، ستحدث حالة تجاوز سعة المكدس.
إنها تشغل المزيد من الذاكرة مما يؤدي إلى تدهور الأداء العام.
دعونا نفهم البرمجة الديناميكية من خلال مثال.
int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td> </tr><tr><td>Bottom-Up</td> </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let's understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let's understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>