الجبر العلائقي هو لغة استعلام إجرائية. فهو يوفر عملية خطوة بخطوة للحصول على نتيجة الاستعلام. ويستخدم عوامل التشغيل لتنفيذ الاستعلامات.
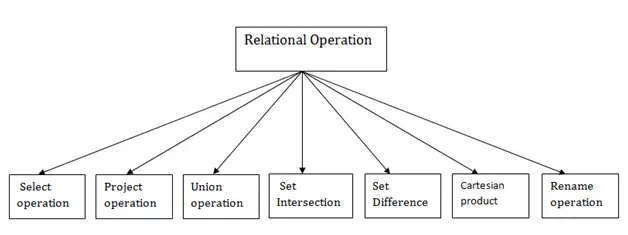
أنواع العمليات العلائقية
1. حدد العملية:
- تحدد عملية التحديد الصفوف التي تلبي المسند المحدد.
- ويشار إليه بـ سيجما (σ).
Notation: σ p(r)
أين:
ص يستخدم للتنبؤ بالاختيار
ص يستخدم للعلاقة
ص تُستخدم كصيغة منطقية افتراضية قد تستخدم موصلات مثل: AND OR وNOT. يمكن استخدام هذه العلاقات كعوامل علائقية مثل =، ≠، ≧، ، ≦.
على سبيل المثال: علاقة القرض
| اسم الفرع | قرض_لا | كمية |
|---|---|---|
| وسط البلد | إل-17 | 1000 |
| الخشب الأحمر | إل-23 | 2000 |
| بيريريد | إل-15 | 1500 |
| وسط البلد | إل-14 | 1500 |
| ميانوس | إل-13 | 500 |
| راوندهيل | إل-11 | 900 |
| بيريريد | إل-16 | 1300 |
مدخل:
σ BRANCH_NAME='perryride' (LOAN)
انتاج:
فرز الفقاعة في جافا
| اسم الفرع | قرض_لا | كمية |
|---|---|---|
| بيريريد | إل-15 | 1500 |
| بيريريد | إل-16 | 1300 |
2. تشغيل المشروع:
- تعرض هذه العملية قائمة تلك السمات التي نرغب في ظهورها في النتيجة. يتم حذف بقية السمات من الجدول.
- ويشار إليه بـ ∏.
Notation: ∏ A1, A2, An (r)
أين
أ1 , A2 , A3 يستخدم كاسم سمة العلاقة ص .
مثال: علاقات العملاء
| اسم | شارع | مدينة |
|---|---|---|
| جونز | رئيسي | هاريسون |
| حداد | شمال | الذرة |
| هايز | رئيسي | هاريسون |
| كاري | شمال | الذرة |
| جونسون | روح | بروكلين |
| بروكس | عضو مجلس الشيوخ | بروكلين |
مدخل:
مامتا كولكارني الممثل
∏ NAME, CITY (CUSTOMER)
انتاج:
| اسم | مدينة |
|---|---|
| جونز | هاريسون |
| حداد | الذرة |
| هايز | هاريسون |
| كاري | الذرة |
| جونسون | بروكلين |
| بروكس | بروكلين |
3. عملية الاتحاد:
- لنفترض أن هناك صفين R وS. تحتوي عملية الاتحاد على جميع المجموعات الموجودة إما في R أو S أو كليهما في R & S.
- فهو يزيل الصفوف المكررة. ويشار إليه بـ ∪.
Notation: R ∪ S
يجب أن تتوفر في العملية النقابية الشرط التالي:
- يجب أن يكون لـ R وS السمة لنفس الرقم.
- يتم التخلص من الصفوف المكررة تلقائيًا.
مثال:
علاقة المودع
| اسم الزبون | الحساب_رقم |
|---|---|
| جونسون | أ-101 |
| حداد | أ-121 |
| مايز | أ-321 |
| تيرنر | أ-176 |
| جونسون | أ-273 |
| جونز | أ-472 |
| ليندسي | أ-284 |
علاقة الاقتراض
| اسم الزبون | قرض_لا |
|---|---|
| جونز | إل-17 |
| حداد | إل-23 |
| هايز | إل-15 |
| جاكسون | إل-14 |
| كاري | إل-93 |
| حداد | إل-11 |
| ويليامز | إل-17 |
مدخل:
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
انتاج:
| اسم الزبون |
|---|
| جونسون |
| حداد |
| هايز |
| تيرنر |
| جونز |
| ليندسي |
| جاكسون |
| كاري |
| ويليامز |
| مايز |
4. تحديد التقاطع:
- لنفترض أن هناك مجموعتين R وS. تحتوي عملية التقاطع المحددة على جميع المجموعات الموجودة في كل من R وS.
- ويشار إليه بالتقاطع ∩.
Notation: R ∩ S
مثال: باستخدام جدول المودع أعلاه وجدول الاقتراض
مدخل:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
انتاج:
| اسم الزبون |
|---|
| حداد |
| جونز |
5. تحديد الفرق:
- لنفترض أن هناك صفين R وS. تحتوي عملية التقاطع المحددة على جميع المجموعات الموجودة في R ولكن ليس في S.
- ويشار إليه بالتقاطع ناقص (-).
Notation: R - S
مثال: باستخدام جدول المودع أعلاه وجدول الاقتراض
مدخل:
الهاشماب في جافا
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
انتاج:
| اسم الزبون |
|---|
| جاكسون |
| هايز |
| ويليامز |
| كاري |
6. المنتج الديكارتي
- يتم استخدام المنتج الديكارتي لدمج كل صف في جدول واحد مع كل صف في الجدول الآخر. ومن المعروف أيضا باسم المنتج المتقاطع.
- ويشار إليه بـ X.
Notation: E X D
مثال:
موظف
اجتياز الطلب المسبق
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | حداد | أ |
| 2 | هاري | ج |
| 3 | جون | ب |
قسم
| DEPT_NO | DEPT_NAME |
|---|---|
| أ | تسويق |
| ب | مبيعات |
| ج | قانوني |
مدخل:
EMPLOYEE X DEPARTMENT
انتاج:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | حداد | أ | أ | تسويق |
| 1 | حداد | أ | ب | مبيعات |
| 1 | حداد | أ | ج | قانوني |
| 2 | هاري | ج | أ | تسويق |
| 2 | هاري | ج | ب | مبيعات |
| 2 | هاري | ج | ج | قانوني |
| 3 | جون | ب | أ | تسويق |
| 3 | جون | ب | ب | مبيعات |
| 3 | جون | ب | ج | قانوني |
7. إعادة تسمية العملية:
يتم استخدام عملية إعادة التسمية لإعادة تسمية علاقة الإخراج. ويشار إليه ب rho (ع).
مثال: يمكننا استخدام عامل إعادة التسمية لإعادة تسمية علاقة STUDENT بـ STUDENT1.
ρ(STUDENT1, STUDENT)
